Il calcolo delle probabilità è quella branca della matematica e della statistica che ci permette di valutare numericamente la possibilità che una certa situazione accada assegnandole un numero da 0 a 1. Minore è questo numero, minore saranno le chances che la situazione in esame si verifichi (diremo che sarà meno probabile); viceversa, man mano che tale valore si avvicina ad 1 l'evento si dirà essere più probabile. Ad esempio, potremmo chiederci "qual è la probabilità che lanciando due volte un dado equilibrato venga fuori il numero 3 e 6" oppure "qual è la probabilità che di estrazione di una pallina rossa da un'urna che contiene 7 palline rosse e 4 nere" e molte altre domande ancora la cui risposta viene fornita dal calcolo combinatorio.
Se vuoi approfondire il concetto di probabilità, ti rimando alla pagina contenente le diverse definizioni di probabilità che i nostri antenati hanno formulato.
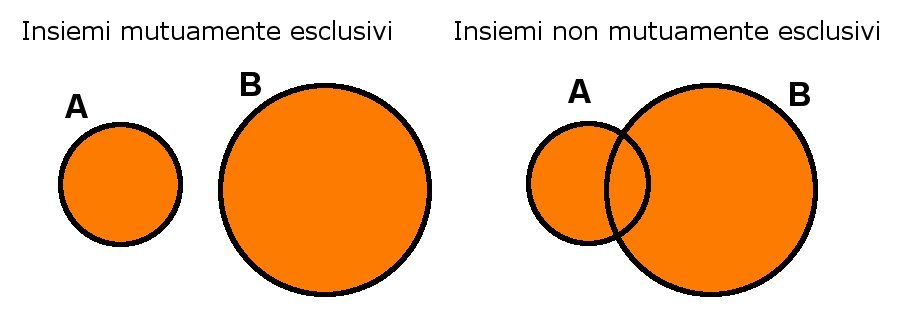
Per poter risolvere qualsiasi problema di probabilità, è prima di tutto necessario saper descrivere completamente lo spazio degli eventi, ossia definire quali sono tutti i possibili casi che possono verificarsi e le relazioni che intercorrono tra loro. Spesso capita che il verificarsi di un evento dipenda dall'esito di un altro e in tal caso bisogna ricorrere alla probabilità condizionata. Diverso è invece il caso di eventi indipendenti in cui l'esito di ciascuno di essi prescinde da quello degli altri.
In alcune situazioni più complesse, dove lo spazio campione è composto da diversi eventi, ci viene in aiuto il Teorema di Bayes, il quale, sotto le ipotesi del Teorema sulla Probabilità Totale, ci consente di calcolare il valore di una probabilità condizionata partizionando lo spazio campione in eventi incompatibili ed esaustivi.
In stretta relazione con la probabilità è il calcolo combinatorio. Esso offre 3 strumenti utili per contare il numero di casi favorevoli o equiprobabili in un dato problema di probabilità oppure semplicemente per contare il numero di raggruppamenti di n oggetti in k classi:
Qui sotto, trovi l'elenco dettagliato delle lezioni di calcolo delle probabilità. In alternativa puoi andare direttamente agli esercizi.
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
