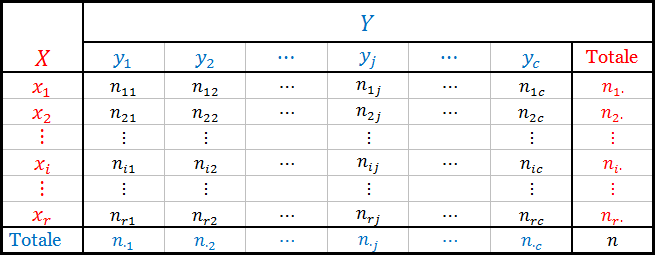
L'indice di Mortara è un indice utilizzato per misurare il grado di connessione o associazione tra due variabili X e Y qualitative nominali o categoriali. Studiare la connessione tra due variabili categoriche vuol dire studiare la loro dipendenza statistica a partire da una tabella a doppia entrata contenente le frequenze osservate o empiriche come quella che ti mostro qui sotto
Ti ho parlato in maniera approfondita delle tabella a doppia entrata o di contingenza in questa lezione.
Ribadisco la notazione usata in tabella:
- r e c sono rispettivamente numero di righe e di colonne e anche numero di modalità di X e di Y.
- $x_i$ e $y_j$ sono le modalità o categorie di X e Y rispettivamente.
- $n_{ij}$ sono le frequenze assolute osservate.
- $n_{i\cdot}$ e $n_{\cdot j}$ sono i totali di riga e di colonna rispettivamente.
- $n$ è il totale delle frequenze assolute $n_{ij}$.
La formula per calcolare l'indice di Mortara è la seguente:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sum\limits_{i,j}\cfrac{|n_{ij}-\hat{n}_{ij}|}{n}}$$ dove $\hat{n}_{ij}$ sono le frequenze teoriche.
Dalla sua forma si può osservare che l'indice di Mortara rappresenta la media aritmetica delle contingenze assolute in valore assoluto. Infatti, è anche chiamato indice di contingenza media assoluto.
Procedura di calcolo dell'indice di Mortara
Calcola le frequenze teoriche o attese $\hat{n}_{ij}$
Le frequenze attese sono quelle che si ottengono nel caso teorico di perfetta indipendenza e si calcolano facendo il prodotto tra totale di riga e di colonna e dividendolo per il totale assoluto: $$\hat{n}_{ij}=\cfrac{n_{i\cdot}*n_{\cdot j}}{n}$$ da calcolare per ogni riga i e colonna $j$ della tabella delle frequenze osservate.
Calcola le contingenze assolute in valore assoluto $|C_{ij}|$
Si calcolano facendo la differenza in valore assoluto tra frequenze osservate e teoriche: $$|C_{ij}|=|n_{ij}-\hat{n}_{ij}|$$ Le contingenze assolute rappresentano l'attrazione (se $C_{ij} >0$) o la repulsione (se $C_{ij} <0$) tra le modalità dei due caratteri X e Y.
Somma le contingenze assolute in valore assoluto e dividi per $n$
Ottieni così la formula dell'indice di Mortara che ti ho riportato sopra.
Proprietà e intepretazione dell'indice di Mortara
Si dimostra che l'indice di Mortara assoluto varia tra 0 e 2, dove il caso limite 0 indica il caso di perfetta indipendenza mentre il caso limite 2 indica perfetta dipendenza stocastica tra X e Y. Inoltre, il valore massimo che assume l'indice di Mortara può essere calcolato mediante la seguente formula: $$M_{max}=2\cdot min\left[\left(1-\cfrac{1}{r}\right), \left(1-\cfrac{1}{c}\right)\right]$$ Osservando che il valore del minimo tra le due quantità tra parentesi può essere al più 1, si capisce perché l'indice di Mortara non può andare oltre 2.
Indice di Mortara normalizzato
Tuttavia, per ottenere una misura relativa della connessione, è necessario normalizzare l'indice di Mortara assoluto che ti ho fornito nella primo paragrafo di questo articolo: $$M_N=\cfrac{M}{M_{max}}$$ In pratica basta dividere il coefficiente di Mortara assoluto per il valore massimo che lo stesso può assumere.
Essendo l'indice di Mortara relativo o normalizzato compreso tra 0 e 1, possiamo valutare il grado di associazione tra X e Y. Praticamente, più è vicino a 0 e minore è l'associazione, mentre invece più si avvicina a 1 maggiore è l'associazione.
Clicca nel bottone in fondo pagina se vuoi scaricare esercizi sul calcolo e l'interpretazione dell'indice di Mortara per una tabella di contingenza.
Altri indici di connessione
L'indice di Mortara è solo uno degli indici di connessione utilizzati in statistica. Uno di questi è sicuramente il chi-quadrato. Vai a leggere l'articolo in cui te ne ho parlato in dettaglio.
Ho anche preparato un esercizio sul calcolo dell'indice di Mortara mediante l'uso di Excel. Cliccaci su se vuoi scaricarlo.



