Considerando l'esperimento che consiste nel lancio di una moneta, i risultati possibili sono T(testa) o C(croce), cioè uno degli elementi dell'insieme $\{T,C\}$.
Se invece consideriamo come esperimento, il lancio di un dato, i possibili risultati sono quelli dell'insieme $\{1,2,3,4,5,6\}$.
Diciamo, quindi spazio campione l'insieme S di tutti i possibili risultati di un esperimento casuale. Uno spazio campione è finito se è composta da un numero finito di elementi come ad esempio lo spazio campione corrispondente al lancio di un dado:
$$S=\{1,2,3,4,5,6\}$$
Diremo, invece, spazio campione infinito quell'insieme formato da infiniti elementi; il numero di volte che bisogna lanciare un dado per ottenere 6, rappresenta un esempio di spazio campione infinito.
Definiamo evento un sottoinsieme E dello spazio campione S ($E\subseteq S$).
Esempio
Si effettuano due lanci consecutivi di una moneta; lo spazio campione è:
$$S=\{TT,CC,TC,CT\}$$L'evento che si verifica quando si presenta una sola volta T è il sottoinsieme:
$$E_1=\{TC,CT\}$$L'evento che si verifica quando si presenta la prima volta T è il sottoinsieme:
$$E_2=\{TT,TC\}$$Notiamo che anche l'intero spazio S è un evento e si chiama evento certo. Ad esempio, nel lancio di un dado, l'evento certo è che esca uno dei numeri $\{1,2,3,4,5,6\}$. Anche l'insieme vuoto $\emptyset$ è un evento ed è detto evento impossibile.
Dal momento che gli eventi sono degli insiemi, analogamente all'algebra degli insiemi, possiamo definire un'algebra per gli eventi usando le operazioni insiemistiche.
Se A e B sono due eventi si S, allora:
- UNIONE: $A\cup B$ è l'evento "A oppure B oppure entrambi"
- INTERSEZIONE: $A\cap B$ è l'evento "sia A che B"
- COMPLEMENTARE: $\overline{A}$ è l'evento "non A"
- DIFFERENZA: $A-B$ è l'evento "A ma non B"
Due eventi A e B sono mutuamente esclusivi, o incompatibili, se non possono verificarsi contemporaneamente.
Da questa definizione, si capisce che se due eventi sono mutuamente esclusivi, saranno pure disgiunti, ossia $A\cap B=\emptyset$. Tramite i Diagrammi di Venn illustriamo qui in basso il concetto:
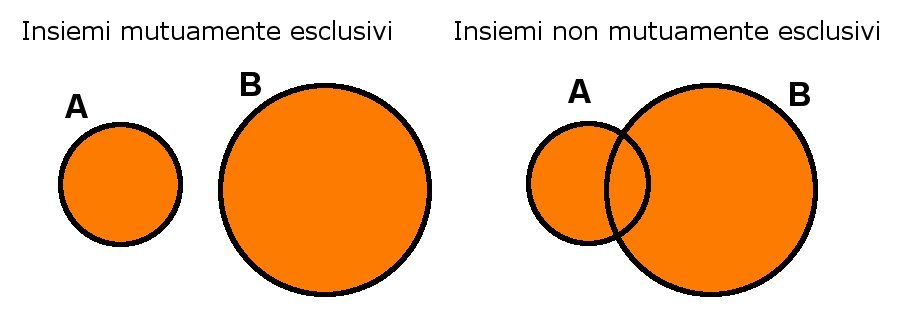
Proprietà delle operazioni insiemistiche
- PROPRIETÀ COMMUTATIVA DI $\cup$ E $\cap$ $$A\cup B=B\cup A\quad\quad A\cap B=B\cap A$$
- PROPRIETÀ ASSOCIATIVA DI $\cup$ E $\cap$ $$A\cup(B\cup C)=(A\cup B)\cup C\quad\quad A\cap(B\cap C)=(A\cap B)\cap C$$
- PROPRIETÀ DISTRIBUTIVA DI $\cup$ RISPETTO A $\cap$ $$A\cup(B\cap C)=(A\cup B)\cap (A\cup C)$$
- PROPRIETÀ DISTRIBUTIVA DI $\cap$ RISPETTO A $\cup$ $$A\cap(B\cup C)=(A\cap B)\cup (A\cap C)$$
- LEGGI DI DE MORGAN $$\overline{A}\cup\overline{B}=\overline{(A\cap B)}$$ $$\overline{A}\cap\overline{B}=\overline{(A\cup B)}$$



