Il Chi-quadrato è l'indice di connessione più utilizzato in statistica per valutare l'associazione tra due variabili categoriali o qualitative.
Ad esempio, supponi di avere le seguenti due variabili:
- X: variabile SESSO le cui modalità sono "maschio" (M) e "femmina" (F).
- Y: variabile PROFESSIONE le cui modalità sono "impiegato", "operaio" e "libero professionista".
Studiare l'associazione o la connessione tra X e Y infatti significa capire se la professione praticata dipende statisticamente dal genere maschio o femmina. Bada bene che la dipendenza stocastica è diversa dalla dipendenza lineare la quale invece si studia calcolando il coefficiente di correlazione.
Lo studio della connessione tra due caratteri qualitativi si basa sul calcolo del chi-quadrato, in simboli $\chi^2$. Se vuoi capire come nasce il chi-quadrato vai a leggere l'articolo in cui parlo della distribuzione del chi-quadrato. Se invece non ti importa la teoria del chi-quadrato e vuoi concentrarti sulla pratica prosegui con la lettura.
Procedura per il calcolo del chi-quadrato
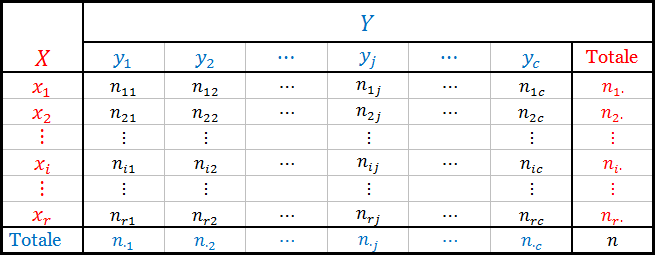
Negli esercizi, si dispone di una tabella di contingenza (vedi figura qui in basso) con $r$ righe e $c$ colonne in cui sono presenti:
- le modalità o categorie di X, $x_i$;
- le modalità o categorie di Y, $y_j$;
- le frequenze osservate $n_{ij}$ (ad esempio $n_{12}$ è la frequenza osservata di riga 1 e colonna 2);
- le frequenze marginali di riga (frequenze totali di riga $n_{i\cdot}$ );
- le frequenze marginali di colonna (frequenze totali di colonna $n_{\cdot j}$);
- il totale $n$ delle frequenze.
REGOLA PER NON CONFONDERSI CON I PEDICI: il primo numerino a pedice indica la riga mentre il secondo la colonna.
Ti illustro adesso i passi per calcolare il chi-quadrato.
Calcolare le frequenze attese o teoriche
Basta moltiplicare i totali di riga per i totali di colonna e dividere per il totale assoluto: $\hat{n}_{ij}=\cfrac{n_{i\cdot}\cdot n_{\cdot j}}{n}$.
Calcolare le contingenze assolute
Le contingenze assolute si calcolano sottraendo le frequenze attese a quelle osservate: $c_{ij}=n_{ij}-\hat{n}_{ij}$.
Elevare al quadrato le contingenze assolute e dividerle per le frequenze teoriche
In formule: $\cfrac{c_{ij}^2}{\hat{n}_{ij}}$.
Calcolare il chi-quadrato
Infine, somma le frazioni calcolate al punto precedente: $\chi^2=\sum\limits_{i,j}\cfrac{c_{ij}^2}{\hat{n}_{ij}}$. Nota che i valori da sommare sono $r\times c$, esattamente il numero di elementi contenuti in una tabella con r righe e c colonne.
Riassumendo, la formula completa del chi-quadrato è:$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\chi^2=\sum\limits_i^r\sum\limits_j^c\frac{(n_{ij}-\hat{n}_{ij})^2}{\hat{n}_{ij}}}$$
Di seguito trovi un esempio numerico sul calcolo del chi-quadrato che ti chiarirà le idee.
Supponiamo di avere la seguente matrice di dati con righe $r=2$ e colonne $c=3$:

Facendo riferimento alla tabella $n_{1\cdot}=51$, $n_{2\cdot}=49$ sono le frequenze marginali di riga (ovvero le somma delle frequenze attese per le righe 1 e 2); $n_{\cdot 1}=25$, $n_{\cdot 2}=50$, $n_{\cdot 3}=25$ sono le frequenze marginali di colonna (ovvero le somme delle frequenze attese per le colonne 1, 2 e 3); e $n=100$ è il totale di tutte le frequenze.
Utilizziamo la procedura di calcolo del chi-quadrato descritta sopra.
- Calcoliamo le frequenze attese $\hat{n}_{ij}$: $$\begin{eqnarray} \hat{n}_{11}&=& \frac{n_{1\cdot}\cdot n_{\cdot 1}}{n}=\frac{51\cdot 25}{100}=12.75\\ \hat{n}_{12}&=&\frac{n_{1\cdot}\cdot n_{\cdot 2}}{n}=\frac{51\cdot 50}{100}=25.50\\ \hat{n}_{13}&=&\frac{n_{1\cdot}\cdot n_{\cdot 3}}{n}=\frac{51\cdot 25}{100}=12.75\\ \hat{n}_{21}&=&\frac{n_{2\cdot}\cdot n_{\cdot 1}}{n}=\frac{49\cdot 25}{100}=12.25\\ \hat{n}_{22}&=&\frac{n_{2\cdot}\cdot n_{\cdot 2}}{n}=\frac{49\cdot 50}{100}=24.50\\ \hat{n}_{23}&=&\frac{n_{2\cdot}\cdot n_{\cdot 3}}{n}=\frac{49\cdot 25}{100}=12.25\end{eqnarray}$$
- Calcoliamo le contingenze assolute $c_{ij}$:$$\begin{eqnarray}
c_{11}&=& n_{11}-\hat{n}_{11}=10-12.75=-2.75\\
c_{12} &=& n_{12}-\hat{n}_{12}=31-25.50=5.50\\
c_{13} &=& n_{13}-\hat{n}_{13}=10-12.75=-2.75\\
c_{21} &=& n_{21}-\hat{n}_{21}=15-12.25=2.75\\
c_{22} &=& n_{22}-\hat{n}_{22}=19-24.50=-5.50\\
c_{23} &=& n_{23}-\hat{n}_{23}=15-12.25=2.75\end{eqnarray}$$ - Eleviamo le contingenze assolute al quadrato dividendole per le frequenze teoriche: $$\begin{eqnarray}
\frac{c_{11}^2}{\hat{n}_{11}}&=& \frac{2.75^2}{12.75}=0.59\\
\frac{c_{12}^2}{\hat{n}_{12}}&=& \frac{5.50^2}{25.50}=1.19\\
\frac{c_{13}^2}{\hat{n}_{13}}&=& \frac{2.75^2}{12.75}=0.59\\
\frac{c_{21}^2}{\hat{n}_{21}}&=& \frac{2.75^2}{12.25}=0.62\\
\frac{c_{22}^2}{\hat{n}_{22}}&=& \frac{5.50^2}{24.50}=1.23\\
\frac{c_{23}^2}{\hat{n}_{23}}&=& \frac{2.75^2}{12.25}=0.62\end{eqnarray}$$ -
Calcoliamo il chi-quadrato sommando i valori calcolati al punto 3: $$\chi^2=0.59+1.19+0.59+0.62+1.23+0.62=4.84$$
Formula operativa del Chi-quadrato
Come visto nell'esempio, il calcolo del Chi-quadrato prevede lunghi e noiosi calcoli che sarebbe meglio snellire soprattutto se ti viene data una tabella a doppia entrata con diverse righe e colonne. Eccoti allora la formula più veloce del Chi-quadrato: $$\chi^2=n\left(\sum\limits_i^r \sum\limits_j^c\cfrac{n_{ij}^2}{n_{i\cdot}\cdot n_{\cdot j}}-1\right)$$
Ma cosa ha di veloce questa formula? Beh, sono due le motivazioni che la rendono più semplice da applicare da un punto di vista computazionale:
- Al numeratore non elevi al quadrato una differenza ma un'unico valore (quindi risparmi il calcolo delle differenze tra frequenze osservate e attese).
- Al denominatore non hai più le frequenze attese ma il prodotto delle marginali (quindi risparmi il calcolo delle frequenze attese).
Ti consiglio di usare quest'ultima formula se il tuo esame è scritto e non puoi fare uso di software quali Excel o R Studio.
Proprietà del Chi-quadrato
Il Chi-quadrato è un indice che assume sempre valori non negativi, maggiori o uguali a zero dato che il suo calcolo prevede la somma di quantità positive. Ma questo indice gode di altre caratteristiche che ti elenco qui di seguito:
- Assume valore massimo pari a $\chi_{max}^2=n[min(r-1,c-1)]$, dove r e c sono rispettivamente il numero di righe e di colonne della tabella iniziale.
- Il range di valori possibili del Chi-quadrato va da 0 a $\chi_{max}^2$, quindi: $0\leq\chi^2\leq\chi_{max}^2$.
- Quando il Chi-quadrato è uguale a 0 si ha la MASSIMA INDIPENDENZA e quindi CONNESSIONE NULLA tra X e Y.
- Quando il Chi-quadrato è uguale a $\chi_{max}^2$ si ha la MASSIMA DIPENDENZA e quindi MASSIMA CONNESSIONE tra X e Y.
- Il Chi-quadrato è un indice simmetrico, nel senso che non tiene conto della direzione della dipendenza (causa-effetto) e rimane invariato se scambiamo il ruolo di X e Y.
Interpretazione statistica del Chi-quadrato
Ti starai già chiedendo come faccio a interpretare il valore del Chi-quadrato che sta all'interno del range descritto nella proprietà 2 dato che negli esercizi il Chi-quadrato non risulta quasi mai uguale a 0 oppure al suo valore massimo. Hai due alternative:
- Usa questa semplice regola: se il valore del Chi-quadrato è più vicino a 0, allora dirai che c'è una scarsa connessione tra X e Y, mentre invece se il valore risulta più prossimo a $\chi_{max}^2$ allora dirai che sussiste una buona associazione tra X e Y.
- In alternativa, calcola un indice relativo o normalizzato.
Un altro modo è quello di condurre un test di ipotesi che si basa sul calcolo del Chi-quadrato, il cosiddetto test di indipendenza del Chi-quadrato.
Indici di connessione relativi
Il calcolo di indici relativi ti permette di valutare il grado di connessione tra le due variabili categoriche. Ne esistono diversi e te li elenco qui sotto.
Indice Chi-quadrato normalizzato $\chi_N^2$
Non è altro che il rapporto tra il Chi-quadrato e il suo valore massimo: $$\chi_N^2=\cfrac{\chi^2}{\chi_{max}^2}=\cfrac{\chi^2}{n\cdot min[(r-1),(c-1)]}$$
Essendo un indice relativo, é compreso tra 0 e 1. Valori del Chi-quadrato normalizzato vicini a 0 indicano scarsa associazione mentre valori vicini a 1 indicano buona associazione tra X e Y.
Indice V di Cramer
È l'indice di connessione relativo più utilizzato ed è dato dalla radice quadrata del rapporto tra il Chi-quadrato e il suo valore massimo. In altre parole, l'indice V di Cramer è la radice quadrata del Chi-quadrato normalizzato: $$V=\sqrt{\cfrac{\chi^2}{n\cdot min[(r-1),(c-1)]}}=\sqrt{\chi_N^2}$$. Anche questo indice varia tra 0 e 1 e valori superiori a 0,2 indicano una buona dipendenza tra X e Y. Facendo riferimento all'esempio numerico di cui sopra l ha: $$\begin{eqnarray}V&=&\sqrt{\cfrac{4,84}{100\cdot min[(2-1),(3-1)]}}=\\&=&\sqrt{\cfrac{4,84}{100\cdot min (1,3)}}=\\&=&\sqrt{\cfrac{4,84}{100}}=0,22\end{eqnarray}$$
Questo vuol dire che i due caratteri, sesso e tipo di lavoro, hanno un grado di associazione del 22%.
Altri indici di connessione
Il Chi-quadrato non è l'unico indice di connessione utilizzato in statistica. Esiste infatti l'indice di Mortara che se vuoi puoi approfondire cliccando qui e l'indice di contingenza media quadratica che è il rapporto tra il Chi-quadrato e il numero totale $n$ delle osservazioni: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{\Phi=\cfrac{\chi^2}{n}}$$
Infine, esistono altri indici di associazione che, oltre a misurare il grado di associazione tra i caratteri, misurano anche il verso della relazione: stiamo parlando dell'indice gamma di Goodman (utilizzato se i valori in tabella sono pochi) e dell'indice di Sperman (utilizzato se i valori in tabella sono più di 11).



