Se sei già esperto nel risolvere le equazioni logaritmiche e vuoi passare alla risoluzione delle disequazioni logaritmiche, in questa pagina ne puoi trovare tante risolte. Di seguito trovi i testi di quelle proposte.
$$(x^2-3x+2)\log(4x-x^2)>0$$
Determiniamo le condizioni di esistenza della funzione logaritmica ponendo l'argomento del log maggiore di 0. Se non ricordi come si risolvono le disequazioni di secondo grado clicca qui per ripassarle.
$$\begin{array}{l} 4x-x^2>0\quad\Rightarrow\quad x^2-4x < 0\\ x(x-4)=0\quad\Rightarrow\quad x=0,\ x=4\end{array}$$
Pertando le C.E. sono $0 < x < 4$.
La disequazione proposta si risolve ponendo entrambi i fattori moltiplicativi maggiori di 0:
La 1) si risolve trovando le soluzioni dell'equazione associata:
$$x_{1,2}=\frac{3\pm\sqrt{9-8}}{2}=\frac{3\pm 1}{2}$$
Si ottengono così due radici dall'equazione associata: $x=1,\ x=2$. Pertanto le soluzioni della disequazione 1) sono i valori esterni: $x<1\ \vee\ x>2$.
Risolviamo la 2) riscrivendo lo zero a secondo membro come $\log 1$ e risolvendo:
$$\begin{array}{l}
\log(4x-x^2)>\log 1\\
4x-x^2-1>0\\
x^2-4x+1 < 0\end{array}$$
Risolvendo l'equazione associata a quest'ultima disequazione si ottiene $x=2\pm\sqrt{4-1}=2\pm\sqrt{3}$. Dunque, le soluzioni della disequazione 2) sono i valori interni: $2-\sqrt{3} < x < 2+\sqrt{3}$.
Adesso, mettiamo a prodotto dei segni le soluzioni di 1) e 2) come mostra il seguente grafico:
Si ha, dunque, $2-\sqrt{3} < x < 1\ \vee\ 2 < x < 2+\sqrt{3}$. Di tale soluzione, dobbiamo prenderne solo la parte che soddisfa le C.E. inizialmente calcolate, ovvero bisogna svolgere il seguente sistema:
$$\begin{cases} 2-\sqrt{3} < x < 1\ \vee\ 2 < x < 2+\sqrt{3}\\ 0 < x < 4\end{cases}$$
il cui risultato è $0 < x < 1\ \vee\ 2 < x < 2+\sqrt{3}$.
$$1+\log_{\frac{1}{2}}\frac{8x-4}{x^2+x}>0$$
Tale disequazione è equivalente al sistema:
$$\left\{\begin{array}{l} \cfrac{8x-4}{x^2+x}>0\\ 1+\log_{\frac{1}{2}}\cfrac{8x-4}{x^2+x}>0\end{array}\right.$$
La prima è la condizione di esistenza del logaritmo ed è una disequazione fratta che si risolve ponendo numeratore e denominatore maggiori di 0:
$\begin{array}{l}
N:\ 8x-4>0\\
x>\cfrac{4}{8}\\
x>\frac{1}{2}\end{array}$
$\begin{array}{l}
D:\ x^2+x>0\\
x(x+1)>0\\
x < -1\ \vee\ x>0\end{array}$
Facciamo il prodotto dei segni di queste due ultime disequazioni trovate:
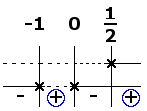
Prendendo la parte positiva, la disequazione fratta è soddisfatta per:
$$-1 < x < 0\ \vee\ x >\frac{1}{2}$$
Risolviamo la seconda disequazione del sistema iniziale:
$$\begin{array}{l}
1+\log_{\frac{1}{2}}\cfrac{8x-4}{x^2+x}>0\\
\log_{\frac{1}{2}}\cfrac{8x-4}{x^2+x}>-1\\
\log_{\frac{1}{2}}\cfrac{8x-4}{x^2+x}>\log_{\frac{1}{2}}\left(\cfrac{1}{2}\right)^{-1}\\
\log_{\frac{1}{2}}\cfrac{8x-4}{x^2+x}>\log_{\frac{1}{2}}2\end{array}$$
A questo punto possiamo togliere i logaritmi ricordandoci che, quando la base è compresa tra $0$ e $1$, il verso della disequazione cambia:
$$\begin{array}{l}
\cfrac{8x-4}{x^2+x}<2\\
\cfrac{8x-4}{x^2+x}-2 < 0\\
\cfrac{8x-4-2x^2-2x}{x^2+x} < 0\\
\cfrac{-2x^2+6x-4}{x^2+x} < 0\end{array}$$
Risolviamo la disequazione fratta ottenuta, ossia:
$\cfrac{-2x^2+6x-4}{x^2+x} < 0$
$\begin{array}{l}
N:\ -2x^2+6x-4>0\\
x^2-3x+2 < 0\\
1 < x < 2\end{array}$
$\begin{array}{l}
D:\ x^2+x>0\\
x < -1\ \vee\ x>0\end{array}$
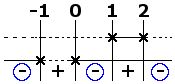
Prendendo la parte negativa del grafico, la seconda disequazione è soddisfatta per:
$$x < -1\ \vee\ 0 < x < 1\ \vee\ x > 2$$
Il sistema iniziale è così pronto per essere risolto:
$$\left\{\begin{array}{l} \frac{8x-4}{x^2+x}>0\\ 1+\log_{\frac{1}{2}}\frac{8x-4}{x^2+x}>0\end{array}\right.$$
$$\left\{\begin{array}{l} -1 < x < 0\ \vee\ x >\frac{1}{2}\\ x < -1\ \vee\ 0 < x < 1\ \vee\ x > 2\end{array}\right.$$
La soluzione della disequazione iniziale è quindi:
$$\cfrac{1}{2} < x < 1\ \vee\ x > 2$$
Oppure analogamente si può scrivere: $$]1/2,1[\ \cup\ ]2,+\infty[$$
$$2^{\frac{x^2-11}{x+2}} < 4$$
Riscrivendo $4$ come $2^2$ la disequazione data è soddisfatta se e soltanto se è soddisfatta la seguente disequazione:
$$\frac{x^2-11}{x+2} < 2$$
In sostanza, la disuguaglianza tra due funzioni esponenziali è soddisfatta se e solo se è soddisfatta la disuguaglianza tra i rispettivi esponenti. Risolviamo, quindi, la disequazione appena ottenuta.
$\frac{x^2-11}{x+2}-2 < 0\quad\Rightarrow\quad \frac{x^2-11-2x-4}{x+2} < 0 \quad\Rightarrow\quad \frac{x^2-2x-15}{x+2} < 0$
Quest'ultima disequazione di tipo fratta:
$\frac{x^2-2x-15}{x+2} < 0\quad\Rightarrow\quad \begin{array}{l} x^2-2x-15 > 0\quad\Rightarrow\quad x < -3\ \vee x > 5\\ x+2 > 0\quad\Rightarrow\quad x>-2\end{array}$
Mettiamo a prodotto dei segni le due soluzioni ottenute:
Considerando solo le regioni negative del grafico, avremo che le soluzioni della disequazione iniziale sono:
$$x < -3\ \vee\ -2 < x < 5\quad\quad\mbox{oppure analogamente}\quad\quad ]-\infty,-3[\ \cup\ ]-2,5[$$
