In questo articolo ti spiego come risolvere una disequazione di secondo grado intera (ossia a coefficienti reali e aventi l'incognita x solo al numeratore).
Se conosci già la teoria puoi saltare agli esercizi svolti cliccando sul bottone qui in basso
Ogni disequazione di secondo grado può essere ricondotta alla forma normale
$$ax^2+bx+c\underset{\le}{\ge}0\mbox{ con } a\neq 0\quad (\large\star)$$
In pratica, la forma normale è quella in cui compaiono solamente i tre termini del trinomio:
- Termine quadratico $ax^2$
- Termine di primo grado $bx$
- Termine noto $c$
Saper risolvere una disequazione di questo tipo significa saper stabilire il segno che assume il trinomio $ax^2+bx+c$
Esistono due metodi per studiare il segno di un trinomio di secondo grado:
- metodo algebrico
- metodo grafico (con parabola)
Metodo algebrico
Questo metodo si basa essenzialmente sull'utilizzo di uno schema semplificativo che io chiamo schema del delta. Eccolo:
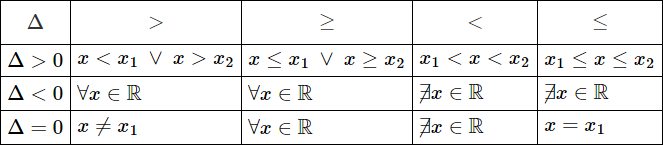
Tale tabella fornisce le soluzioni della disequazione di secondo grado a seconda del verso e del segno del delta. Fai attenzione però! Per poter utilizzare questo schema prima di tutto devi assicurarti che il coefficiente $a$ sia positivo! Se fosse negativo cambia i segni di tutti i coefficienti e inverti il verso della disequazione.
Di seguito ti mostro come usare questo schema, quindi continua a leggere se vuoi scoprirlo!
Prima però è necessario distinguere due tipi di disequazioni di secondo grado:
- Disequazioni di secondo grado complete (quelle in cui appaiono tutti e tre i coefficienti a,b,c)
- Disequazioni di secondo grado incomplete (quelle in cui non appaiono almeno uno tra i due coefficiente b e c)
Faccio questa distinzione perché nel primo caso userò la formula del delta mentre nel secondo ti farò vedere che non è necessario e che puoi trovare velocemente le soluzioni risparmiando tempo e fatica.
Disequazione di secondo grado completa
Supposto $a>0$, i passaggi da seguire per la risoluzione di disequazioni di secondo completa sono essenzialmente 3:
Calcola il delta
Calcola il discriminante $\Delta=b^2-4ac$.
Trova le radici dell'equazione associata
Se il $\Delta$ è maggiore o uguale a 0, l'equazione associata $ax^2+bx+c=0$ ha due soluzioni reali distinte (se $\Delta>0$) o coincidenti (se $\Delta=0$). Per ulteriori dettagli circa la risoluzione di un'equazione di secondo grado leggi questo approfondimento Equazioni di secondo grado). Ricorda che nel caso di delta negativo l'equazione associata non ha soluzioni, quindi salta al punto successivo.
Guarda la tabella del delta
Incrocia la riga con il segno del delta (maggiore, minore o uguale a 0) e la colonna contenente il verso della disequazione data. La cella che vai così a beccare contiene la soluzione della disequazione di secondo grado assegnata.
Esempio 1
Risolvere la seguente disequazione di secondo grado $$x^2-4x-5>0$$
Risolviamo la disequazione proposta esaminando dapprima il segno di $\frac{\Delta}{4}$:
$$\frac{\Delta}{4}=\left(\frac{b}{2}\right)^2-ac=2^2-[1\cdot (-5)]=4+5=9>0$$
Poiché il delta è maggiore di $0$, l'equazione associata alla nostra disequazione ($x^2-4x-5=0$) ha due soluzioni reali e distinte. Calcoliamole usando la formula risolutiva ridotta per le equazioni di secondo grado:
$$x_{1,2}=2\pm\sqrt{9}=2\pm 3$$
Dunque, le soluzioni dell'equazione sono $x_1=2-3=-1$ e $x_2=2+3=5$.
Dallo schema riassuntivo visto sopra, intercettando la cella corrispondente a $\Delta>0$ e verso della disequazione $>$, troviamo le soluzioni della disequazione data:
$$x<-1\ \vee\ x>5$$
che possono essere riscritte sotto forma di intervallo:
$$]-\infty, -1[\ \cup\ ]5,+\infty[$$
Per risolvere una disequazione di secondo grado incompleta, come detto, non è necessario applicare la formula del delta. Ti ho fatto lo stesso discorso quando ti ho spiegato le equazioni di secondo grado incomplete. Di seguito ti mostro come risolvere le disequazioni di secondo grado incomplete sia pure che spurie.
Disequazioni di secondo grado pure (b=0)
Una disequazione si dice pura se manca il termine con la x di primo grado, ossia si presenta nella forma generica $$ax^2+c\underset{\le}{\ge}0\ (\large\star\large\star)$$ la cui equazione associata $ax^2+c=0$ può essere risolta come risolviamo le EQUAZIONI DI PRIMO GRADO, ossia isolando la $x$ al primo membro: $$ax^2=-c\ \Rightarrow\ x^2=-\frac{c}{a}$$ e applicando infine la radice quadrata ad ambo i membri: $$x=\pm\sqrt{-\frac{c}{a}}$$
Dall'ultima espressione ottenuta si capisce che se il termine sotto radice $-\frac{c}{a}$ è negativo, il tutto non avrebbe senso, ossia l'equazione associata è impossibile ($\Delta < 0$). In questo caso la soluzione della disequazione $(\large\star\large\star)$ sarà una tra quelle presenti nella seconda riga della solita tabella. Il verso della disequazione, identificherà univocamente tale soluzione.
Esempio 2
Risolvere la seguente disequazione di secondo grado $$25-x^2>0$$
Innanzitutto mettiamo in ordine i termini della disequazione:
$$-x^2+25>0$$
Inoltre, facciamo in modo che il coefficiente di $x^2$ diventi positivo, moltiplicando ambo i membri per $-1$:
$$x^2-25 < 0$$
Come fatto nell'esempio precedente, calcoliamo il segno del delta quarti:
$$\frac{\Delta}{4}=0-(-25)=25>0$$
Calcoliamo le due soluzioni reali e distinte:
$$x_{1,2}=\pm\sqrt{25}=\pm 5$$
Infine, andando a leggere lo schema riassuntivo in corrispondenza della riga con $\Delta >0$ e verso $<$ scriviamo le soluzioni della disequazione mediante gli operatori di disuguaglianza
$$-5 < x < 5$$
e sotto forma di intervallo
$$]-5,5[$$
Occhio agli errori frequenti che si compiono su questo tipo di disequazioni! Ho registrato un video in cui te ne parlo in dettaglio.
Disequazioni di secondo grado spurie (c=0)
Si tratta di una disequazione di secondo grado senza termine noto, cioè della forma $$ax^2+bx\underset{\le}{\ge}0\ (\large\star\large\star\large\star)$$
Risolviamo la sua equazione associata mettendo a fattor comune la $x$: $$ax^2+bx=0\ \Rightarrow\ x\cdot(ax+b)=0\begin{array}{l} \nearrow\\ \searrow\end{array} \begin{array}{l} x= 0\ \\ \\ ax+b=0\ \Rightarrow\ x=-\frac{b}{a}\end{array}$$
In questo caso, poiché l'equazione associata ha due soluzioni distinte dovrà essere $\Delta > 0$, il che vuol dire che la soluzione della disequazione $(\large\star\large\star\large\star)$ giacerà sulla prima riga della tabella risolutiva. Analogamente ai casi precedenti, identificando il verso della disequazione, possiamo risalire alla sua soluzione guardando appunto la tabella risolutiva.
Esempio 3
Risolvere la seguente disequazione di secondo grado $$x^2-5x < 0$$
Risolviamo l'equazione associata: $$x^2-5x=0\ \Rightarrow\ x(x-5)=0\begin{array}{l} \nearrow\\ \searrow\end{array} \begin{array}{l} x= 0\ \\ \\ x-5=0\ \Rightarrow\ x=5\end{array}$$
Dunque, poichè le soluzioni dell'equazione associata sono distinte $\Delta > 0$ e dato che il verso della disequazione è $<$, le soluzione saranno quelle interne (prima riga, 3 colonna della tabella risolutiva): $$0 < x < 5$$ oppure sotto forma di intervallo: $$]0,5[$$
Disequazioni di secondo grado monomie (b=c=0)
Per concludere, ti spiego l'ultimo tipo di disequazione di 2° grado nelle quali sicuramente ti sei già imbattuto o ti imbatterai a breve se hai già iniziato a studiare il segno di trinomi di secondo grado. Sto parlando della disequazione che contiene solo il termine $ax^2$. In questo caso è immediato trovare le soluzioni distinguendo 4 casi. Per semplicità suppongo che $a>0$.
Disequazione monomia con verso maggiore (>)
La disequazione $ax^2>0$ ha come radici tutti i valori di $x$ eccetto 0 ($x\neq 0$) dato che il termine $ax^2$ è positivo per tutti i valori reali $x$ diversi da 0.
Si potrebbe ragionare anche con lo schema, osservando che il delta di una equazione monomia è uguale a 0 e che, in questo caso, il verso è maggiore. Leggendo lo schema ricaveremmo $x\neq x_1$, ossia $x\neq 0$.
Esempio 4
$$3x^2>0$$
Dividendo per 3 ambo i membri la disequazione diventa $x^2>0$ la cui unica radice è $x\neq 0$. Infatti, troviamo tale soluzione nella tabella incrociando la riga con $\Delta = 0$ con la colonna con il verso $>$.
Disequazione monomia con verso maggiore o uguale ($\geq$)
La disequazione $ax^2\geq0$ è verificata per tutti i valori di $x$ dato che il termine $ax^2$ è positivo o uguale a zero per qualsiasi valore reale $x$.
Si potrebbe ragionare anche con lo schema, osservando che il delta di una equazione monomia è uguale a 0 e che il verso della disequazione è $\geq$. Infatti, incrociando riga e colonna dello schema si ottiene $\forall x\in\mathbb{R}$.
Esempio 5
$$\cfrac{1}{2}x^2\geq 0$$
Moltiplicando per $\cfrac{1}{2}$ ambo i membri la disequazione diventa $x^2\geq 0$ la quale è sempre soddisfatta (per ogni valore sostituito al posto dell'incognita $x$) dato che una quantità al quadrato è sempre maggiore o uguale a 0.
Disequazione monomia con verso minore (<)
La disequazione $ax^2<0$ non ha radici perché il termine $ax^2$ è sempre maggiore o uguale a 0, per tutti i valori reali di$x$.
Si potrebbe arrivare alla stessa soluzione osservando che $\Delta = 0$ e il verso della disequazione è $<$. Dallo schema in alto si ricava $\forall x\in\mathbb{R}$.
Esempio 6
$$4x^2<0$$
Dividendo per 4 ambo i membri la disequazione diventa $x^2<0$ che, come detto, non ha soluzioni perché $x^2$ è sempre maggiore o uguale a 0. Quindi scriviamo IMPOSSIBILE oppure $\not\exists x\in\mathbb{R}$.
Disequazione monomia con verso minore o uguale ($\leq$)
La disequazione $ax^2\leq 0$ non è mai soddisfatta eccetto che per $x=0$ dato che il termine di secondo grado $ax^2$ può solo essere 0 e non negativo.
Si potrebbe arrivare alla stessa soluzione osservando che $\Delta = 0$ e il verso della disequazione è $\leq$. Dallo schema in alto si ricava $x=x_1=0$.
Esempio 7
$$5x^2\leq 0$$
Dividendo per 5 ambo i membri la disequazione diventa $x^2\leq 0$ che, come detto, ammette solo la radice 0. Quindi scriviamo $x=0$.
Metodo grafico
Passiamo all'altro metodo di risoluzione mediante il grafico della parabola. Ho registrato un video in cui ti mostro come risolvere le disequazioni di secondo grado con il metodo della parabola.



