Dati i punti $A(1,2)$, $B(-3,0)$ e $C(-1,-3)$ determina le equazioni della dilatazione con centro nell'origine che trasforma i vertici $A$, $B$ e $C$ nei corrispondenti punti di coordinate $A'\left(\frac{1}{2},-1\right)$, $B'\left(-\frac{3}{2},0\right)$ e $C'\left(-\frac{1}{2},-\frac{3}{2}\right)$.
Ricordiamo che le equazioni della dilatazione sono
$$\begin{cases} x'=hx\\ y'=ky\end{cases}$$
Per determinare $h$ e $k$, dobbiamo sostituire le coordinate di $A'$, $B'$ e $C'$ in $x'$ e $y'$, mentre le coordinate di $A$, $B$ e $C$ in $x$ e $y$. Facciamolo solo per i punti $A'$ e $A$ e analogamente si farà le altre due coppie di punti:
$$\begin{cases} \frac{1}{2}=h\cdot 1\\ -1=k\cdot 2\end{cases}\ \Rightarrow\ h=\frac{1}{2},\ k=-\frac{1}{2}$$
Dunque la dilatazione è espressa mediante le seguenti equazioni:
$$\begin{cases} x'=\frac{1}{2}x\\ y'=-\frac{1}{2}y\end{cases}$$
Altri esercizi di matematica

Esercizi sul raccoglimento parziale
Calcolo altezza di un prisma retto con base trapezoidale
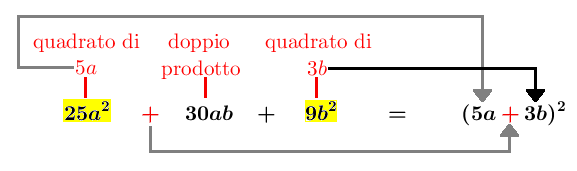
Esercizi sulla scomposizione riconducibile a prodotti notevoli
Solido generato dalla rotazione di un trapezio rettangolo
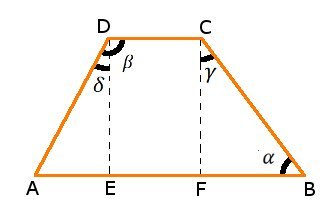
Calcolo lati trapezio scaleno noti basi e angoli

Disequazioni con il valore assoluto risolte

Esercizi svolti con il criterio della radice

Esercizi sulla scomposizione di trinomi di secondo grado

Domini o campi di esistenza di funzioni risolti

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare