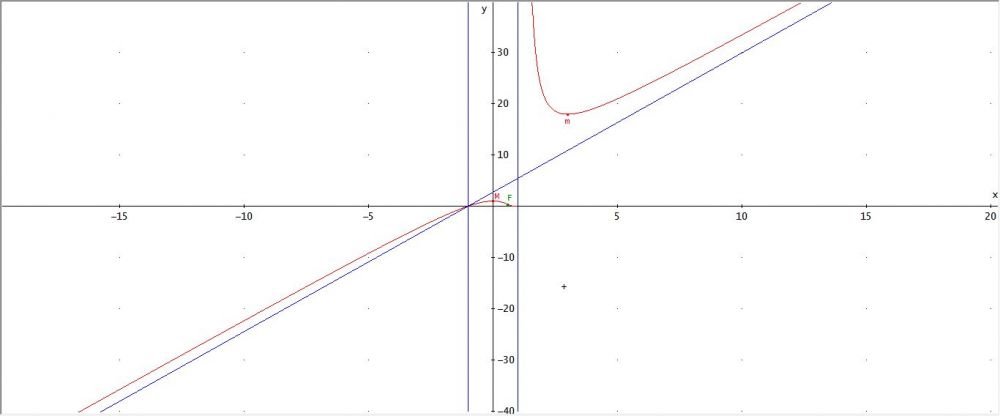
Supponiamo di avere la funzione omografica di equazione:
$$y=\frac{ax+b}{4x+d}$$
passante per i punti $A(1,1)$ e $B(-1,2)$ e con asintoto verticale di equazione $x=-\frac{1}{2}$
Ci poniamo il problema di determinare l'equazione dell'iperbole equilatera, il suo centro di simmetria e i suoi assi di simmetria.
Per trovare l'equazione dell'iperbole dobbiamo ricavarci le incognite $a,\ b,\ \mbox{e}\ d$. Ci possiamo ricavare subito $d$ sapendo che l'asintoto verticale ha equazione $x=-\frac{1}{2}$:
$$x=-\frac{d}{c}=-\frac{d}{4}=-\frac{1}{2}\quad\Leftrightarrow\quad d=\frac{1}{2}4=2$$
Invece, $a$ e $b$ li ricaviamo imponendo all'equazione dell'iperbole il passaggio per i punti $A$ e $B$:
$$\left\{\begin{array}{l} 1=\frac{a+b}{6}\\ -2=\frac{-a+b}{-2}\end{array}\right.\quad\Rightarrow\left\{\begin{array}{l} a+b=6\\ -a+b=4\end{array}\right.\quad\Rightarrow\left\{\begin{array}{l} a=6-b\\ -6+b+b=4\end{array}\right.\quad\Rightarrow\left\{\begin{array}{l} a=6-b\\ 2b=10\end{array}\right.\quad\Rightarrow\left\{\begin{array}{l} a=1\\ b=5\end{array}\right.$$
Dunque, l'equazione dell'iperbole è:
$$y=\frac{x+5}{4x+2}$$
Facilmente troviamo il centro di simmetria:
$$C\left(-\frac{d}{c},\frac{a}{c}\right)=\left(-\frac{1}{2},\frac{1}{4}\right)$$
Per concludere troviamo gli assi di simmetria:
$$y-\frac{a}{c}=\pm\left(x+\frac{d}{c}\right)$$
Il primo sarebbe:
$$y-\frac{a}{c}=x+\frac{d}{c}\quad\Rightarrow\quad y-\frac{1}{4}=x+\frac{1}{2}\quad\Rightarrow\quad y=x+\frac{3}{4}$$
Il secondo invece è:
$$y-\frac{a}{c}=-x-\frac{d}{c}\quad\Rightarrow\quad y-\frac{1}{4}=-x-\frac{1}{2}\quad\Rightarrow\quad y=-x-\frac{1}{4}$$
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
