Scomponi in fattori riconoscendo i prodotti notevoli
- $25a^2-9$
- $\frac{25}{3}a^2-3b^2$
- $(5x-2)^2-4x^2$
- $25a^2+30ab+9b^2$
- $a^4+2a^2b^2+4b^4$
- $x^2-y^2-1-2y$
- $(a+b)^2+4(a+b)+4-b^2$
- $9a^2+4b^2+1-12ab+6a-4b$
- $4a^2+4b^2+c^2+4ab+4ac+4bc$
- $x^3+3x^2+3x+1$
- $8a^3-6a^2b+6ab^2-b^3$
- $8a^3+b^3$
- $x^6+y^3$
Scomposizione mediante somma per differenza
Esercizio 1
$$25a^2-9$$
Essendo $25a^2$ il quadrato di $5a$ e $9$ il quadrato di $3$, possiamo scomporre mediante la differenza di quadrati: $$25a^2-9=(5a+3)(5a-3)$$
Esercizio 2
$$\frac{25}{3}a^2-3b^2$$
In questo caso, bisogna prima raccogliere $\frac{1}{3}$: $$\frac{25}{3}a^2-3b^2=\frac{1}{3}(25a^2-9b^2)=$$
E poi applicare il metodo di scomposizione mediante differenza di quadrati come fatto per il polinomio 1: $$=\frac{1}{3}(5a+3b)(5a-3b)$$
Esercizio 3
$$(5x-2)^2-4x^2$$
Anche qui possiamo scomporre ricordando la scomposizione somma per differenza: $$\begin{array}{l} (5x-2)^2-4x^2=\\ =[(5x-2)+2x][(5x-2)-2x]=\\ =[5x-2+2x][5x-2-2x]=\\ =(7x-2)(3x-2)\end{array}$$
Esercizio 4
$$25a^2+30ab+9b^2$$
Individuiamo i due termini del trinomio che possono essere dei quadrati e ricaviamone le basi: $$25a^2=(5a)^2\quad\mbox{e}\quad 9b^2=(3b)^2$$
Controlliamo che il doppio prodotto delle basi trovate sia uguale all'altro termine del trinomio: $$2(5a\cdot 3b)=30ab$$
Allora possiamo scrivere il trinomio come quadrato del binomio formato dalle due basi trovate, legate dal segno che precede il doppio prodotto: $$25a^2+30ab+9b^2=(5a+3b)^2$$
Qui in basso è schematizzato il procedimento per ricondurre il trinomio ad un quadrato di binomio: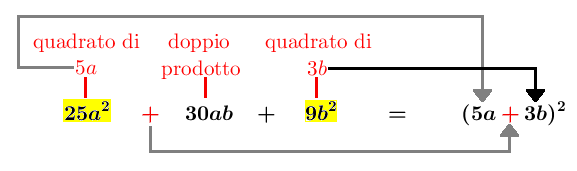
Scomposizione mediante quadrato di binomio
Esercizio 5
$$a^4+2a^2b^2+4b^4$$
Tale trinomio non è il quadrato di un binomio, perchè il doppio prodotto di $a^2$ e $2b^2$ non è $2a^2b^2$, ma $4a^2b^2$. Pertanto non possiamo scomporlo.
Esercizio 6
$$x^2-y^2-1-2y$$
Osserviamo che gli ultimi 3 termini rappresentano lo sviluppo di un quadrato di binomio se mettiamo in evidenza un segno $-$: $$x^2-y^2-1-2y=x^2-(y^2+1+2y)=x^2-(y+1)^2=$$
Notiamo una differenza di quadrati: $$=[x-(y+1)][x+(y+1)]=(x-y-1)(x+y+1)$$
Esercizio 7
$$(a+b)^2+4(a+b)+4-b^2$$
Anche questo, come il polinomio 6, è un esempio di differenza di quadrati quando almeno un quadrato non è un monomio. Quindi, ragionando allo stesso modo si ha: $$\begin{array}{l} (a+b)^2+4(a+b)+4-b^2=\\ =[(a+b)+2]^2-b^2=\\ =[(a+b)+2-b][(a+b)+2+b]=\\ =(a+2)(a+2b+2)\end{array}$$
Esercizio 8
$$9a^2+4b^2+1-12ab+6a-4b$$
Siamo chiaramente in presenza di un polinomio con 6 termini riconducibile al quadrato di un trinomio, come dimostra il ragionamento seguente.
Individuiamo i tre termini del polinomio che possono essere dei quadrati e ricaviamocene le basi: $$9a^2=(3a)^2,\quad 4b^2=(2b)^2,\quad 1=1^2$$
Controlliamo che i valori assoluti dei doppi prodotti siano uguali ai valori assoluti degli altri termini: $$12ab=2(3a\cdot 2b),\quad 6a=2(3a\cdot 1),\quad 4b=2(2b\cdot 1)$$
Analizziamo allora i segni dei doppi prodotti:
1) $3a$ e $2b$ sono discordi poichè il loro prodotto è negativo ($-12ab$)
2) $3a$ e $1$ sono concordi poichè il loro prodotto è positivo ($+6a$)
3) $2b$ e $1$ sono discordi poichè il loro prodotto è negativo ($-4b$)
Dunque, dalla 2. si deduce che $3a$ e $1$ hanno lo stesso segno, mentre dalla 1. e dalla 3. segue che $2b$ ha segno opposto. Abbiamo perciò due possibili scomposizioni: $$\begin{array}{l} 9a^2+4b^2+1-12ab+6a-4b=(3a-2b+1)^2\\ 9a^2+4b^2+1-12ab+6a-4b=(-3a+2b-1)^2\end{array}$$
Esercizio 9
$$4a^2+4b^2+c^2+4ab+4ac+4bc$$
Come prima, si ha: $$4a^2=(2a)^2,\quad 4b^2=(2b)^2,\quad c^2=(c)^2$$
Ci accorgiamo però, che il termine $4ab$ non è il doppio prodotto tra $2a$ e $2b$, infatti: $$2(2a\cdot 2b)=8ab\neq 4ab$$
Dunque il polinomio non è riconducibile al quadrato di trinomio.
Scomposizione mediante cubo di binomio
Esercizio 10
$$x^3+3x^2+3x+1$$
Un polinomio formato da 4 termini può essere riconducibile al cubo di un binomio.
Individuiamo i due termini del quadrinomio che possono essere dei cubi e ricaviamone le basi: $$x^3=(x)^3,\quad 1=1^3$$
Verifichiamo la presenza dei relativi tripli prodotti: $$3x^2=3\cdot x^2\cdot 1,\quad 3x=3\cdot x\cdot 1^2$$
Pertanto: $$x^3+3x^2+3x+1=(x+1)^3$$
Esercizio 11
$$8a^3-6a^2b+6ab^2-b^3$$
Seguiamo lo stesso procedimento cercando di applicare il metodo di scomposizione mediante il cubo di un binomio.
I due termini del quadrinomio che possono essere dei cubi e le loro rispettive basi sono: $$8a^3=(2a)^3,\quad -b^3=(-b)^3$$
Ma il primo triplo prodotto non coincide con il termine $-6a^2b$ infatti: $$3\cdot (2a)^2\cdot (-b)=-12a^2b\neq -6a^2b$$
Dunque il quadrinomio non è riconducibile al cubo di binomio.
Scomposizione mediante somma di cubi
Esercizio 12
$$8a^3+b^3$$
Questo polinomio è la somma di due cubi che si scompone facilmente individuando i due cubi: $$A=2a,\quad B=b$$
Quindi possiamo scrivere: $$\begin{array}{l} 8a^3+b^3=(2a)^3+(b)^3=\\ =(2a+b)[(2a)^2-2ab+b^2]=\\ =(2a+b)(4a^2-2ab+b^2)\end{array}$$
Esercizio 13
$$x^6+y^3$$
Anche per questo polinomio possiamo applicare il metodo di scomposizione mediante la somma di cubi. Infatti i cubi sono: $$A=x^2,\quad B=y$$
Possiamo quindi scomporre la somma di cubi nel modo seguente: $$\begin{array}{l} x^6+y^3=(x^2)^3+y^3=\\ =(x^2+y)(x^4-x^2y+y^2)\end{array}$$








