Calcolo lati trapezio scaleno noti basi e angoli

1. $AB=5\sqrt{3}+21$
2. $CD=9$
3. $\alpha=60^\circ$
4. $\cos\widehat{D}=\cos\beta=-\frac{5}{13}$
5. $DA=?\quad CB=?$

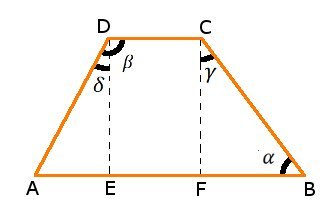
PROCEDIMENTO:

L'angolo $\gamma$ del triangolo $CFB$ misura:

$\gamma=180^\circ-60^\circ-90^\circ=30^\circ$

Inoltre, per le formule sugli angoli associati possiamo scrivere:

$\cos\beta=\cos(90^\circ+\delta)=-\sin\delta=-\frac{5}{13}\quad\quad\Rightarrow\quad\quad \sin\delta=\frac{5}{13}$

Applichiamo il teorema dei seni ai triangoli $AED$ e $CFB$:

$\begin{cases} \frac{AE}{\sin\delta}=\frac{DA}{\sin 90^\circ}\\ \frac{FB}{\sin\gamma}=\frac{FC}{\sin\alpha}\end{cases}$

Ma osservando che:

$FB=AB-AE-EF=5\sqrt{3}+21-9-AE=5+\sqrt{3}+12-AE$

e che

$FC=ED=\sqrt{DA^2-AE^2}$

Il sistema precedente può essere riscritto nel seguente modo:

$\begin{cases} \frac{AE}{\frac{5}{13}}=DA\\ \frac{5+\sqrt{3}+12-AE}{\sin 30^\circ}=\frac{\sqrt{DA^2-AE^2}}{\sin 60^\circ}\end{cases}\quad\quad\Rightarrow\quad\quad \begin{cases} DA=\frac{13}{5}AE\\ \frac{5+\sqrt{3}+12-AE}{\frac{1}{2}}=\frac{\sqrt{\frac{169}{25}AE^2-AE^2}}{\frac{\sqrt{3}}{2}}\end{cases}$

Sviluppando la seconda equazione del sistema otteniamo:

$\begin{array}{l} 5+\sqrt{3}+12-AE=\frac{\sqrt{\frac{169-25}{25}AE^2}}{\sqrt{3}}=\frac{\frac{12}{5}AE}{\sqrt{3}}=\frac{12}{5\sqrt{3}}AE\quad\quad\Rightarrow\\ \Rightarrow\quad\quad \frac{12+5\sqrt{3}}{5\sqrt{3}}AE=5\sqrt{3}+12\quad\quad\Rightarrow\quad\quad AE=5\sqrt{3}\end{array}$

Sostituiamo nella prima equazione del sistema il valore di $AE$ ottenendo così il primo lato obliquo $DA$:

$DA=\frac{13}{5}AE=\frac{13}{5}5\sqrt{3}=13\sqrt{3}$

Calcoliamo inoltre $FB$:

$FB=5\sqrt{3}+12-AE=5\sqrt{3}+12-5\sqrt{3}=12$

Infine, applicando il teorema di Pitagora al triangolo rettangolo $CFB$ otteniamo l'altro lato obliquo $CB$:

$CB=\sqrt{CF^2+FB^2}=\sqrt{144\cdot 3+144}=24$