Dati due numeri reali $h$ e $k$ non nulli, si dice deformazione o dilatazione con centro nell'origine $O$, quella trasformazione geometrica che ad ogni punto $P(x,y)$ associa un punto $P'(x',y')$ tale che:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\begin{cases} x'=hx\\ y'=ky\end{cases}}$$
In particolare,
- se $h=k$ la dilatazione è una omotetia;
- se $h=k=1$ la dilatazione è una identità;
- se $h=k=-1$ la dilatazione è una simmetria rispetto all'origine;
- se $h=-1,\ k=1$ la dilatazione è una simmetria rispetto all'asse $\vec{y}$;
- se $h=1,\ k=-1$ la dilatazione è una simmetria rispetto all'asse $\vec{x}$;
- se $h\neq 1,\ k=1$ si ha una dilatazione orizzontale;
- se $h=1,\ k\neq 1$ si ha una dilatazione verticale.
Da un punto di vista geometrico, la dilatazione è quella trasformazione che trasforma un quadrato unitario in un rettangolo con lati $h$ e $k$, come mostra la figura qui sotto.
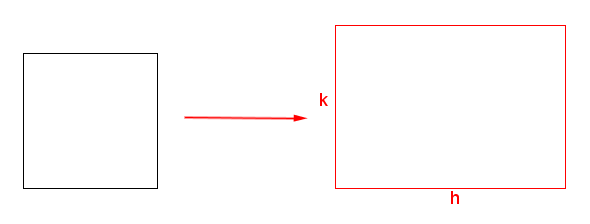
Se il centro della dilatazione non coincide con l'origine ma con il punto $C(x_c,y_c)$, le equazioni diventano:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\begin{cases} x'=h(x-x_c)+x_c\\ y'=k(y-y_c)+y_c\end{cases}}$$
La deformazione gode delle seguenti proprietà:
- Ad eccezioni di casi particolari, l'unico punto unito della deformazione è il suo centro. Quindi, per trovare il centro, quando questo non è l'origine, basta cercare il punto unito;
- se $h\neq\pm 1,\ k\neq\pm 1,\ h\neq k$, le uniche rette unite sono gli assi cartesiani;
- se $F'$ è la corrispondente figura ottenuta dalla deformazione di $F$, vale la seguente relazione tra le loro aree: $$A(F')=hkA(F)$$



