L'asimmetria è una misura di forma proprio perché serve a descrivere la forma della distribuzione di una variabile casuale. Questa, assieme alle misure di tendenza centrale e di dispersione completano la parte di statistica descrittiva.
L'asimmetria viene misurata attraverso un indice numerico chiamato coefficiente di curtosi di Fisher.
Prima di tutto però cosa si intende per simmetria e quali tipi di asimmetria esistono in statistica.
Distribuzioni simmetriche
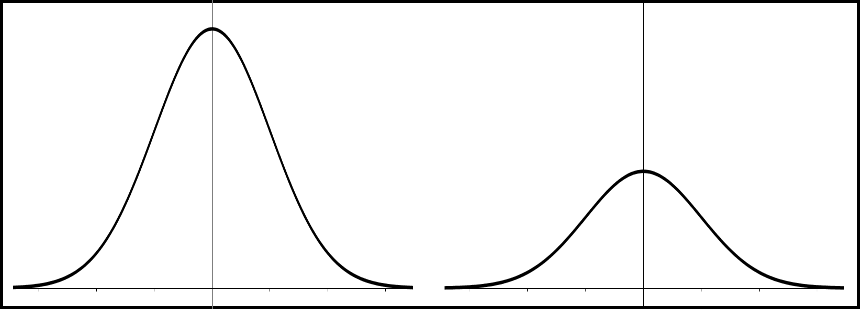
La distribuzione di una variabile casuale è simmetrica se esiste un punto dell'ascissa tale che, tracciando un asse verticale passante per quel punto, la curva risulta speculare rispetto a tale asse, detto asse di simmetria. Le curve qui sotto sono esempi di distribuzioni simmetriche. Per queste vale sempre il fatto che media, moda e mediana coincidono
Asimmetria destra e sinistra
Quando invece la distribuzione presenta code di lunghezza diversa, si parla di asimmetria positiva e asimmetria negativa.

In particolare si ha
- asimmetria positiva o destra quando i dati sono più dispersi verso destra (geometricamente la coda destra è più pronunciata)
- asimmetria negativa o sinistra quando i dati sono più dispersi verso sinistra (geometricamente la coda sinistra è più pronunciata)
Vediamo adesso come si misura l'asimmetria.
Coefficiente di asimmetria di Fisher
Il coefficiente di asimmetria di Fisher misura il grado di asimmetria di una distribuzione ed è definito da $$\bbox[#ffffff,5px,border:2px solid #ff6600]{a=\cfrac{\cfrac{\sum_i(x_i-\overline{x})^3n_i}{\sum_in_i}}{\sigma^3}}$$
dove
- $a$ indica l'indice di asimmetria di Fisher,
- $x_i$ sono i valori della distribuzione
- $\overline{x}$ è il valore medio
- $n_i$ sono le frequenze assolute
- $\sigma$ è lo scarto quadratico medio o deviazione standard della distribuzione.
Osserviamo che se la distribuzione è simmetrica rispetto alla media, il coefficiente di asimmetria è nullo in quanto i termini della sommatoria hanno somma nulla, mentre tanto più la distribuzione è asimmetrica tanto più $a$ è grande in valore assoluto. In particolare:
- Se $a=0$ la distribuzione è perfettamente simmetrica
- Se $a>0$ si ha asimmetria destra
- Se $a < 0$ si ha asimmetria sinistra
Altri indici di forma
In statistica esiste un altro indice di forma utilizzato per misurare la forma di una distribuzione, il coefficiente di curtosi di Pearson. Clicca qui per leggere la lezione che ti ho preparato.



