La media aritmetica è l'indice di posizione, o per meglio dire di centralità, più usato in statistica descrittiva. Talvolta è anche chiamata indicatore di sintesi perché serve a sintetizzare con un solo numero un insieme di dati (per esempio il peso medio o l'altezza media degli studenti di una classe). Si calcola sommando tutti i valori a disposizione e dividendo per il numero totale di valori.
In maniera formale si può dire che la media aritmetica di $n$ dati $x_1,x_2,\dots ,x_n$ è la quantità
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\overline{x}=\frac{\sum\limits_{i=1}^nx_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}}$$
La suddetta è la formula della media aritmetica più utilizzata ma non è l'unica. Infatti, a seconda del tipo di dati che hai, può non essere corretto utilizzarla. In questo articolo ti mostro le 3 formule della media aritmetica e ti spiego in quali casi utilizzare una piuttosto che un'altra:
- Distribuzione di valori singoli (media aritmetica semplice)
- Distribuzione di frequenze per valori singoli (media aritmetica ponderata)
- Distribuzione di frequenze per valori raggruppati in classi (media per dati raggruppati in classi)
Media aritmetica semplice
Questo è il caso che ti ho menzionato sopra, ossia quello in cui devi semplicemente calcolare la media aritmetica di una lista di valori. Definendo
- $n$ il numero dei valori della distribuzione
- $x_i,\ i=0,1,2,\dots , n$ i valori
la media aritmetica si calcola facendo il rapporto tra la somma dei valori $x_i$ e il numero dei valori, ossia:
$$\overline{x}=\cfrac{x_1+x_2+\dots + x_n}{n}\quad (\large\star )$$
Esempio
Le temperature della neve in gradi Celsius di una nota località sciistica nel mese di gennaio sono state le seguenti: $$-4,-3,-2,-1,0,1$$Calcola la temperatura media della neve. Osservando che $n=6$ e applicando la formula che ti ho dato sopra si ottiene: $$\overline{x}=\cfrac{-4-3-2-1+0+1}{6}=-1,5$$La temperatura media della neve è quindi 1,5 gradi Celsius.
Media aritmetica ponderata
La formula della media aritmetica ponderata, detta anche pesata, si utilizza nel caso di una distribuzione di frequenza, ossia una tabella in cui ci sono il numero di occorrenze (frequenze assolute) di ciascun valore che la variabile in esame assume. Si dice anche media aritmetica pesata perché ciascun valore viene moltiplicato per la corrispondente frequenza o peso.
Indicando con
- $k$ il numero di valori distinti che assume la variabile in esame
- $x_i,\ i=1,2,\dots , k$ i valori
- $n_i,\ i=1,2,\dots , k$ le frequenze assolute di ciascun valore
- $n=n_1+\dots +n_k$, la somma totale delle frequenze, ossia il numero totale delle osservazioni.
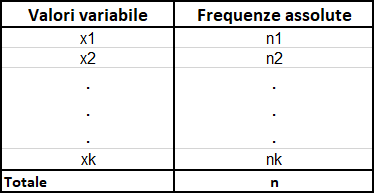
la distribuzione di frequenza della variabile è rappresentata dalla seguente tabella
La formula della media aritmetica ponderata è dunque $$\overline{x}=\cfrac{x_1\cdot n_1+x_2\cdot n_2+\dots +x_k\cdot n_k}{n}$$
Esempio
Supponi che le medie aritmetiche dei voti riportati agli esami di maturità (in sessantesimi) in quattro classi di un istituto superiore siano le seguenti:
Calcola la media aritmetica dei voti di maturità per l’intero istituto.
Banalmente si ha:$$\overline{x}=\cfrac{54\cdot 30+46\cdot 27+40\cdot 20+52\cdot 18}{95}$$
Media aritmetica per dati raggruppati in classi
La media aritmetica si può calcolare anche nel caso in cui i valori sono raggruppati in classi. In questo caso indico con:
- $k$ il numero di classi in cui sono raggruppati i valori della variabile in esame
- $(x_{i-1},x_i)\ i=1,2,\dots , k$ la generica classe $i-$esima
- $n_i,\ i=1,2,\dots , k$ le frequenze assolute di ciascuna classe
- $n=n_1+\dots +n_k$, il totale delle frequenze assolute.
La distribuzione di frequenza in classi è di questo tipo:
Osserva che il simbolo "-|" sta a indicare che l'estremo sinistro della classe è incluso mentre quello destro no. Per calcolare la media ponderata in questo caso è necessario dapprima calcolare i valori centrali $m_i$ delle classi facendo la media aritmetica dei valori estremi di ciascuna classe: $$m_i=\cfrac{x_{i-1}+x_i}{2},\ i=1,2,\dots , k$$ Questi vanno poi moltiplicati per le rispettive frequenze assolute: $$\overline{x}=\cfrac{x_1\cdot m_1+x_2\cdot m_2+\dots +x_k\cdot m_k}{n}$$
Esempio
Supponi di avere la seguente distribuzione del reddito annuo in euro dei 1000 abitanti di un comune
Calcola il reddito medio degli abitanti del comune.
I valori centrali delle classi sono:
$\begin{array}{l}m_1=\cfrac{1000+5000}{2}=3000\\m_2=\cfrac{5000+15000}{2}=10000\\m_3=\cfrac{15000+35000}{2}=25000\\m_4=\cfrac{35000+75000}{2}=55000\end{array}$
La media è quindi: $$\overline{x}=\cfrac{3000\cdot 100+10000\cdot 400+25000\cdot 300+50000\cdot 200}{1000}=22800$$
Quando NON usare la media aritmetica
Come detto all'inizio di questa lezione, la media aritmetica non è un indice robusto perché è fortemente influenzato da valori che si distanziano troppo dal resto della distribuzione. Questi vengono detti outliers o valori anomali. Ad esempio, supponi che la tua variabile oggetto di studio descriva i pesi in kg di 10 studenti di una certa classe di un istituto superiore, ossia: $$53,\ 52,\ 49,\ 60,\ 130,\ 61,\ 58,\ 50,\ 120,\ 55$$
Innanzitutto nota la presenza di valori dei due valori strani, 130 e 120. Dico strani perché questi indicano pesi di persone e inoltre sono molto più grandi del resto dei pesi. Se calcolassi la media aritmetica applicando la formula $(\large\star)$ il peso medio della classe risulterebbe essere $68,8kg$. Se eliminassi i pesi anomali 130 e 120 il peso medio sarebbe $54,75kg$, molto più piccolo rispetto al precedente; infatti la presenza di valori troppo grandi influenza in maniera significativa il valore medio. In tal caso la media aritmetica è una misura distorta (in inglese si dice bias) e quindi non è possibile usarla per descrivere la distribuzione dei pesi degli studenti. Allora quale indice usare quando sono presenti outliers? Eliminare i valori anomali non è sempre la soluzione corretta a meno che non ci siano stati degli errori nella fase di rilevazione dei dati.
La mediana: alternativa alla media aritmetica
In questo caso si utilizza un altro indicatore di posizione chiamato mediana. Questo è un indice di sintesi che rappresenta il valore che spezza la distribuzione in due parti uguali. In altre parole ci dice il valore che occupa la posizione centrale nella distribuzione. A differenza della media, la mediana non è influenzata da valori anomali e quindi è un indice più affidabile. Inoltre, essa corrisponde al secondo quartile. A proposito, in questo articolo ti ho spiegato come calcolarla.
Altri tipi di media
La media aritmetica è senz'altro il tipo di media più diffusa e utilizzata ma non è la sola. Esistono infatti altre medie che si utilizzano in situazioni più particolari. Clicca nei link qui sotto per visualizzare l'articolo in dettaglio.
- Media geometrica
- Media armonica
- Media quadratica