La mediana è uno degli indicatori di sintesi più utilizzati in statistica il cui termine sta per valore di mezzo, ossia rappresenta il valore che occupa la posizione centrale in un insieme di dati. Per tale motivo la mediana è un indice di posizione come media e quartili.
Per calcolare la mediana è necessario innanzitutto disporre i valori in ordine crescente e poi prendere il valore o i valori centrali a seconda del numero di dati a disposizione; si fa infatti la distinzione tra il caso in cui il numero dei valori è pari e il caso in cui invece è dispari. Prosegui la lettura per i dettagli oppure clicca sul bottone qui sotto per accedere agli esercizi sulla mediana.
Di seguito ti insegno come calcolare la mediana nei casi più comuni, quando utilizzarla e perché.
Mediana di un numero dispari di valori
Questo è il calcolo della media più semplice, infatti se il numero dei valori a disposizione è dispari la mediana è esattamente il valore centrale. Leggi l'esempio pratico qui sotto per capire meglio.
Consideriamo i seguenti dati (5 in tutto quindi dispari) $$15,\quad 14,\quad 2,\quad 27,\quad 13$$ e disponiamoli in ordine crescente $$2,\quad 13,\quad 14,\quad 15,\quad 27$$ Risulta che la mediana è il valore 14.
Mediana di un numero pari di valori
Se invece il numero di dati a disposizione è pari, devo considerare i due valori che occupano le posizione centrali e calcolare la media aritmetica.
Consideriamo un numero di dati pari come il seguente $$11,\quad 9,\quad 17,\quad 19,\quad 4,\quad 15$$ e li ordiniamo in maniera crescente $$4,\quad 9,\quad 11,\quad 15,\quad 17,\quad 19$$ I due valori centrali sono 11 e 15, quindi la mediana è la loro media aritmetica: $$Me=\frac{11+15}{2}=13$$
Mediana per dati raggruppati in classi
In questo caso, data una distribuzione di frequenze in classi, bisogna seguire i seguenti step:
- calcolare le frequenze relative;
- calcolare le frequenze cumulate;
- determinare la classe in corrispondenza della quale la frequenza cumulata sia maggiore di $0.5$;
- applicare la formula della mediana per dati raggruppati in classi fornita qui sotto.
Indicata con $[x_{i-1},x_i]$ tale classe (detta classe mediana) e con $f_c^{i-1}$ e $f_c^i$ i valori delle frequenze cumulate corrispondenti, per trovare il valore mediano si applica la seguente formula: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{Me = x_{i-1}+(x_i-x_{i-1})\frac{0.5-f_c^{i-1}}{f_c^i-f_c^{i-1}}}\quad\large\star$$
Per determinare i quartili e i percentili si adatta tale formula (vedi qui).
Esempio
Si considerino le distribuzioni per le classi di età della popolazione residente (espressa in migliaia) in Piemonte nel 1979:
Calcolare l'età mediana nella regione Piemonte.
Qui in basso, la tabella con le frequenze relative e cumulate.

Notiamo subito che il valore della prima frequenza cumulata maggiore di 0.5 è $0.6105$ e si trova in corrispondenza della classe $25-|45$. Quest'ultima è la classe mediana. Per trovare il valore mediano, utilizziamo la formula esposta sopra: $$\begin{array}{l}Me = 25+(45-25)\frac{0.5-0.3316}{0.6105-0.3316}\\=37.0760\end{array}$$
Mediana di una distribuzione marginale o condizionata
Esempio
Consideriamo la tabella doppia dell'esercizio visto qui (clicca per vedere come calcolare la media condizionata).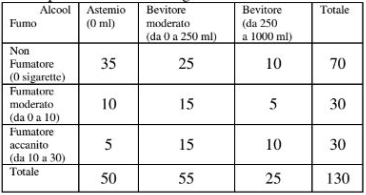
Calcolare la mediana del numero di sigarette fumate dagli astemi e dai bevitori.
Continuiamo a indicare con S la variabile "numero di sigarette fumate" e con A e B rispettivamente i gruppi di persone astemie e bevitori. Ricordiamo che lo studio di una tabella a doppia entrata si effettua lavorando separatamente su ciascuna categoria mostrate nella figura qui sotto
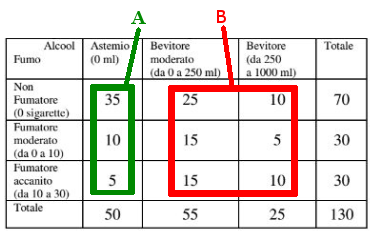
Ricaviamoci le frequenze relative e cumulate del numero di sigarette fumate dagli astemi inglobando il valore 0 nella classe [0,10]:

Osservando che la classe mediana è [0,10], la mediana della distribuzione condizionata del numero di sigarette fumate dagli astemi è data dalla formula $\large\star$: $$\begin{array}{l}Me(S|A)=0+(10-0)\cdot\frac{0.5-0}{0.9-0}\\=5.56\ (\mbox{fumatori})\end{array}$$
Ricaviamoci adesso le frequenze relative e cumulate del numero di sigarette fumate dai bevitori inglobando al solito il valore 0 nella classe [0,10]:

Applicando nuovamente la $\large\star$, otteniamo la mediana del numero di sigarette fumate dai bevitori: $$\begin{array}{l}Me(S|B)=0+(10-0)\cdot\frac{0.5-0}{0.6875-0}\\=7.27\ (\mbox{fumatori})\end{array}$$
Mediana di un trasformazione lineare
La mediana, esattamente come il valore medio, è un indice invariante per trasformazioni lineari, ossia gode della seguente proprietà: $$Me(a\cdot X+b)=a\cdot Me(X)+b$$
Ma cosa significa e come si applica? Te lo faccio capire con il seguente esempio:
Immagina di avere una variabile aleatoria X con mediana pari a 6 e di dover calcolare la mediana di una nuova variabile Y trasformata di X definita come Y=3X+2. Per calcolare la mediana di Y basta calcolare: $$Me(3X+2)=3\cdot Me(X)+2=3\cdot 6+2=20$$
Quando usare la mediana
Fai attenzione a non confondere la mediana con la media. Nonostante siano entrambi degli indici di posizione, hanno significati per diversi. La mediana si usa quando l'insieme di dati a disposizione ha una variabilità elevata e/o presenta valori che si distaccano troppo dal resto (i famosi outlier). In questi casi, usare la media sarebbe sbagliato perché questa sarebbe influenzata da valori troppo grandi o troppo piccoli come ti ho spiegato in fondo all'articolo della media aritmetica. Sia mediana che outliers sono valori che caratterizzano il boxplot. Te ne ho parlato qui in dettaglio.
Perché calcolare la mediana
Come detto la mediana è un indice di centralità non distorto (e quindi più robusto rispetto alla media aritmetica) perché non influenzato da valori estremi presenti nei dati. Il suo calcolo può essere utile per descrivere meglio un fenomeno. Nel caso in cui media e mediana di una certa variabile fossero uguali o simili, risulterebbe più semplice interpretare quel valore. Ad esempio, se la mediana e la media dei pesi degli studenti di una classe si aggira intorno ai 70kg diremo che il peso medio degli studenti è 70kg.



