La curtosi misura il maggiore o minore appiattimento di una curva rispetto alla curva normale o curva di Gauss ed è un indice di forma valido per curve unimodali (con una sola moda) tendenzialmente simmetriche. Non confonderlo con un altro indice di forma , l'asimmetria, di cui te ne ho parlato in questa pagina.
La curtosi si misura mediante il coefficiente di curtosi di Pearson la cui formula è: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{K=\cfrac{\cfrac{\sum_i(x_i-\overline{x})^4n_i}{\sum_in_i}}{\sigma^4}-3}$$
dove
- $K$ indica l'indice di curtosi,
- $x_i$ sono i valori della distribuzione
- $\overline{x}$ è il valore medio
- $n_i$ sono le frequenze assolute
- $\sigma$ è la deviazione standard o scarto quadratico medio della distribuzione.
La curtosi ci dice quanto la curva della distribuzione si allontana da quella di una normale. Più propriamente:
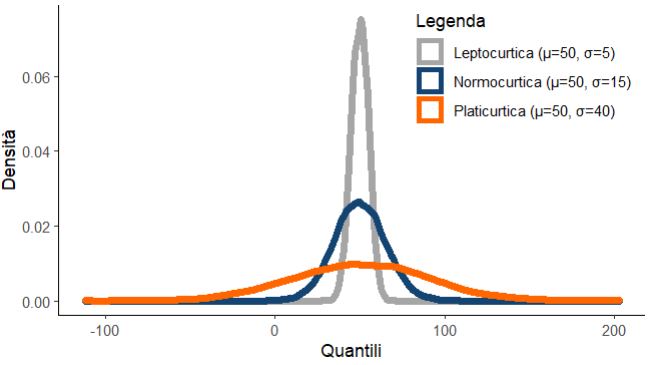
- Se $K=0$ la curva si definisce normocurtica o mesocurtica (distribuzione normale)
- Se $K > 0$ la curva si definisce leptocurtica (più appuntita della normale)
- Se $K < 0$ la curva si definisce platicurtica (più piatta della normale)