In statistica, la moda di un insieme di dati è il valore o la classe con la massima frequenza assoluta. In parole più semplici, la moda rappresenta il valore della distribuzione che compare con maggiore frequenza. La moda è un indice di posizione come media e mediana.
Inoltre, la moda può essere calcolata sia per variabili quantitative numeriche che per variabili categoriali o qualitative.
Moda di dati semplici
Se si ha una lista di valori numerici, la moda si calcola prendendo quel valore che occorre più volte.
La moda dell'insieme dei dati $$3, 3, 5, 4, 7, 7, 7, 9, 2, 1$$ è $\widetilde{x}=7$ perché 7 è il valore che compare più volte rispetto agli altri.
Come detto sopra, è anche possibile calcolare la moda per variabili qualitative.
Supponiamo di voler calcolare la moda della variabile "colore degli occhi" che è distribuita come segue:
MARRONI NERI VERDI AZZURRI MARRONI AZZURRI MARRONI VERDI NERI MARRONI NERI AZZURRI
Moda in una distribuzione di frequenza
Alcune i volte i dati sono un pò troppi e contare le occorrenze dei valori non risulta proprio comodo. In questi casi i dati possono essere organizzati in una tabella delle frequenze che semplifica il calcolo della moda. Ad esempio, posso decidere di organizzare in tabella i dati degli esempi precedenti:
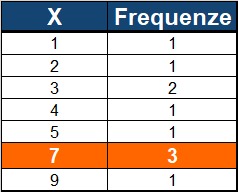
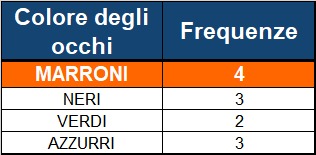
Si vede come, dal conteggio delle frequenze, risulta immediato il calcolo della moda.
Distribuzioni bimodali e plurimodali
Un insieme di dati che presenta più di una moda è detto bimodale. Ad esempio, l'insieme di dati $$3,3,3,5,4,7,7,7,9,2,1$$ ha due mode $\widetilde{x}=3$ e $\widetilde{x}=7$. Le distribuzioni che hanno più di due mode si dicono plurimodali.
Classe modale
Nel caso in cui i dati sono raggruppati in classi, non è possibile trovare un singolo valore modale bensì una classe modale. Ad esempio, la seguente tabella riporta la distribuzione di 100 imprese artigianali lombarde secondo il numero X di dipendenti.
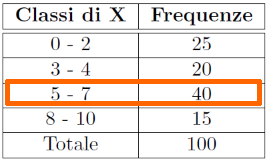
La classe con maggior frequenza è 5-7, la quale rappresenta la classe modale.
Rappresentazione grafica della moda
La moda è anche detto indice di forma (come i coefficienti di asimmetria) perché ci fornisce informazioni circa la forma della distribuzione, in particolare indica il punto più alto della distribuzione. Questo è dovuto al fatto che la moda, essendo la modalità più frequente è anche quella più probabile.
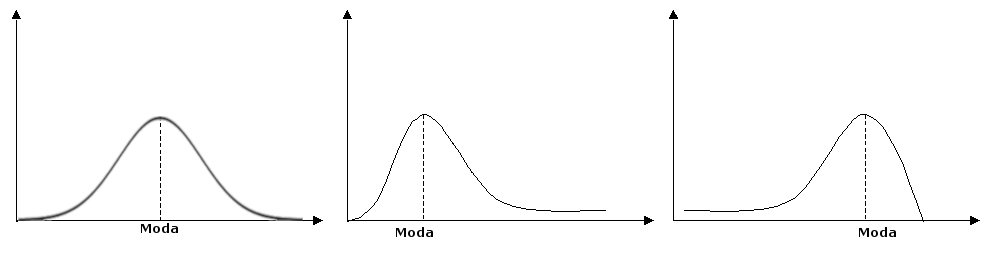
Esistono anche insiemi di dati che non hanno moda. Ad esempio il seguente insieme di dati $$3,5,4,7,8,6,9,2,1$$ non ha moda, perché ogni dato si presenta una sola volta.



