La deviazione standard è un indice di dispersione molto utilizzato in statistica per misurare la variabilità di una variabile o di un fenomeno statistico oggetto di studio. Molto spesso la si confonde con la varianza: nota invece che la deviazione standard è la radice quadrata della varianza!
Di seguito ti mostro due modi per calcolare la deviazione standard. Se invece vuoi andare direttamente agli esercizi svolti clicca sul bottone:
Calcolare la deviazione standard: formula teorica
Per definizione la deviazione standard è la radice quadrata del rapporto tra la somma degli scostamenti al quadrato dei valori dalla media ($(x_i-\overline{x})^2) e il numero $n$ di osservazioni. In formule:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\cfrac{\sum\limits_{i=1}^n (x_i-\overline{x})^2}{n}}}$$
la quale possiamo riscrivere come:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\cfrac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+\dots +(x_n-\overline{x})^2}{n}}}$$
Dalla formula che ti ho appena dato puoi capire il motivo per cui la deviazione standard è anche chiamata scarto quadratico medio. Infatti:
- gli scarti sono le varie differenze dei valori dalla media: $x_i-\overline{x}$
- gli scarti quadratici sono gli scarti al quadrato: $(x_i-\overline{x})^2$
- infine, scarto quadratico medio perché si divide la somma degli scarti per il numero di osservazioni $n$.
Si può dire dunque che la deviazione standard è la media aritmetica degli scarti quadratici sotto radice. Inoltre, ribadisco la relazione che intercorre tra varianza e deviazione standard, ossia la varianza si ottiene calcolando il quadrato della deviazione standard:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma^2=\cfrac{\sum\limits_{i=1}^n (x_i-\overline{x})^2}{n}}$$
Questa che ti ho dato però è la formula che rispecchia esattamente la definizione di deviazione standard, quindi una formula prettamente teorica. Per calcolare la deviazione standard negli esercizi si utilizza una formula più pratica che agevola notevolmente i calcoli.
Calcolare la deviazione standard: formula operativa
Si dimostra che la somma dei quadrati degli scarti matematicamente equivale alla differenza tra la somma dei quadrati dei valori ($x_i^2$) e il prodotto del numero di osservazioni $n$ e il valore medio al quadrato $\overline{x}^2$. Cioè, si ha:
$$\sum\limits_{i=1}^n (x_i-\overline{x})^2=\sum\limits_{i=1}^n (x_i)^2-n\cdot\overline{x}^2$$
Questo risultato ci consente di poter calcolare in modo molto più semplice la deviazione standard:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\cfrac{\sum\limits_{i=1}^n (x_i)^2-n\cdot\overline{x}^2}{n}}}\quad\LARGE\star$$
Al solito, sviluppando la sommatoria avremo:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\cfrac{x_1^2+x_2^2+\dots +x_n^2-n\cdot\overline{x}^2}{n}}}$$
Calcoliamo la deviazione standard dei seguenti numeri: 8 6 3 4.5 9 2
1) Calcolo la media aritmetica: $$\overline{x}=\cfrac{8+6+3+4.5+9+2}{6}=5.42$$
2) Calcolo la somma dei quadrati dei valori: $$\sum\limits_{i=1}^6 (x_i)^2=8^2+6^2+3^2+4.5^2+9^2+2^2=214.25$$
3) Calcolo la varianza con la formula operativa: $$\sigma^2=\cfrac{214.25-6\cdot 5.42^2}{6}=6.33$$
4) Calcolo la deviazione standard facendo la radice: $$\sigma=\sqrt{6.33}=2.52$$
Deviazione standard di dati raggruppati
Finora ho fatto riferimento a dati semplici, ossia una lista di valori numerici. Alcune volte i dati possono essere organizzati in classi e inseriti in una tabella di frequenza. In questo caso bisogna usare la formula della deviazione standard per dati raggruppati:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\cfrac{\sum\limits_{i=1}^k (x_i-\overline{x})^2\cdot n_i}{n}}}$$
dove $k$ sono le classi, $n_i$ sono le frequenze assolute di ogni classe ed $n$ la somma totale delle frequenze assolute.
Anche in questo caso puoi usare la formula veloce $\LARGE\star$ riadattata al caso di dati raggruppati:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\cfrac{\sum\limits_{i=1}^k (x_i)^2\cdot n_i-n\cdot\overline{x}^2}{n}}}$$
la quale, sviluppando la sommatoria, diventa:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{\sigma=\sqrt{\cfrac{x_1^2\cdot n_1+x_2^2\cdot n_2+\dots +x_k^2\cdot n_k-n\cdot\overline{x}^2}{n}}}$$
Vuoi vedere degli esempi di calcolo della deviazione standard in questo particolare caso? Vai agli esercizi svolti cliccando sul bottone qui in basso.
Deviazione standard della popolazione $\sigma$ o campionaria $s$?
Molto spesso si fa confusione tra deviazione standard riferita ai dati di un'intera popolazione e deviazione standard di un campione, ossia di una parte rappresentativa della popolazione. Come detto in questo articolo la popolazione rappresenta l'insieme completo dei dati che descrivono un fenomeno statistico, mentre il campione è sottoinsieme di dati estratti dalla popolazione. Focalizziamoci sulla notazione simbolica e sulle formule da utilizzare in riferimento ai due concetti.
Quando si parla di deviazione standard della popolazione ci riferiamo alla $\sigma$ che ho calcolato nel paragrafo precedente, mentre invece quando stai esaminando un insieme più ristretto di dati (un campione), ci riferiamo alla deviazione standard campionaria che si indica con $s$. In termini di formule non c'è differenza. Tuttavia, $s$ non essendo uno stimatore corretto della varianza della popolazione, viene molto spesso rimpiazzata con la deviazione standard campionaria corretta.
Deviazione standard campionaria corretta
La deviazione standard corretta $s_c$ viene utilizzata nella statistica inferenziale (intervalli di confidenza e test di ipotesi per intenderci). La sua formula è molto simile a quella di $s$ o $\sigma$; l'unica differenza sta al denominatore in cui si mette $n-1$ piuttosto che $n$:
$$\bbox[#ffffff,5px,border:2px solid #ff6600]{s_c=\sqrt{\cfrac{\sum\limits_{i=1}^n (x_i)^2-n\cdot\overline{x}^2}{n-1}}}$$
Puoi altresì ricavare la deviazione standard campionaria corretta a partire dalla deviazione standard campionaria mediante la seguente formula: $$s_c=s\cdot\cfrac{n}{n-1}$$
Banalmente la varianza campionaria corretta non è altro che la deviazione standard campionaria corretta elevata al quadrato: $$s_c^2=\cfrac{\sum\limits_{i=1}^n (x_i)^2-n\cdot\overline{x}^2}{n-1}$$
Come leggere la deviazione standard in un istogramma
Ti stai chiedendo come capire se la deviazione standard di una variabile è piccola o grande leggendo un istogramma? Guarda l'immagine qui in basso.
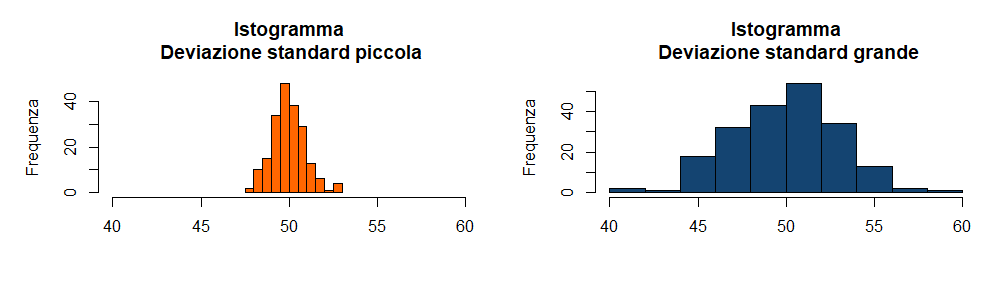
Come vedi nel primo grafico le barre sono più concentrate attorno al valore 50 mentre nel secondo sono più disperse attorno a tale valore. Questo vuol dire che nel primo istogramma la deviazione standard è minore rispetto al secondo.
Come leggere la deviazione standard in un boxplot
La misura della dispersione può essere letta anche da un boxplot. Ti ho parlato in dettaglio di questo grafico in questo articolo. In un boxplot maggiore è la larghezza della scatola e la lunghezza dei baffi, maggiore sarà la deviazione standard. Guarda l'immagine in basso.
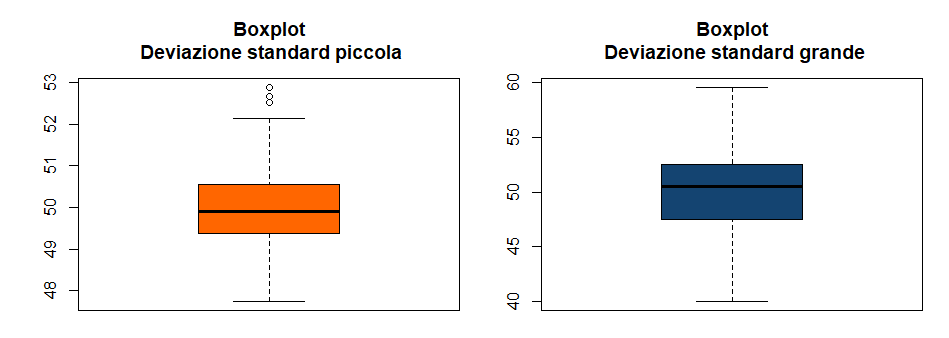
Apparentemente sembra che i due boxplot non differiscano di molto ma se osservi la scala numerica presente a sinistra del grafico puoi notare alcune differenze. Ad esempio, la scatola del primo grafico va da poco più di 49 a poco più di 50 mentre la scatola del secondo grafico va da 47 a 53 circa. Allo stesso modo puoi osservare anche la differenza nella lunghezza dei baffi. Diremo dunque che nel primo grafico la variabilità è maggiore.
La deviazione standard rappresenta inoltre la misura di variabilità maggiormente utilizzata rispetto ad altri indici di dispersione come il campo di variazione e lo scostamento medio semplice.



