Date le seguenti equazioni cartesiane, verificare se esse rappresentano delle trasformazioni geometriche e motivarne la risposta:
$$(1)\begin{cases} x'=2x-y+1\\ y'=4x+2y-1\end{cases}\quad (2)\begin{cases} x'=2x+y\\ y'=4x+2y-3\end{cases}$$
Ricordiamo che una trasformazione geometrica è una corrispondenza biunivoca che associa a ogni punto del piano un punto stesso del piano.
Dunque, per verificare che (1) e (2) siano delle trasformazioni geometriche, dobbiamo riscrivere i sistemi cercando di ricavarci $x$ e $y$, ovvero, effettuiamo la trasformazione inversa.
Esplicitando $x$ e $y$ dalla (1) otteniamo le seguenti equazioni: $$\begin{cases} x=\frac{1}{4}x'+\frac{1}{8}y'-\frac{1}{8}\\ y=-\frac{1}{2}x'+\frac{1}{4}y'+\frac{3}{4}\end{cases}$$
Dunque la (1) definisce una trasformazione geometrica.
Dalla (2) invece, otteniamo:
$$\begin{cases} 0=x'-\frac{1}{2}y'-\frac{3}{2}\\ x=\frac{1}{4}y'-\frac{1}{2}y+3\end{cases}$$
le quali non definiscono in modo univoco le coordinate $x$ e $y$, per cui la (2) non è una trasformazione geometrica.
Altri esercizi di matematica
Calcolo angolo in un settore circolare

Esercizio sull'affinità inversa e calcolo dei suoi punti uniti
Calcolo angolo in un rettangolo circoscritto a un triangolo
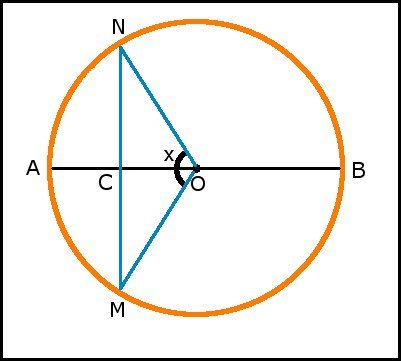
Misura dell'angolo al centro di una circonferenza

Funzione trigonometrica definita a tratti unif. continua

Simmetria assiale e calcolo dell'asse di simmetria

36 studi di funzioni ad una variabile risolti
Disequazioni di secondo grado svolte

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare