In un parallelogramma ABCD, si considerano due punti P e Q sul lato AD. Dimostrare che i triangoli BPC e BQC che si formano, sono equivalenti.
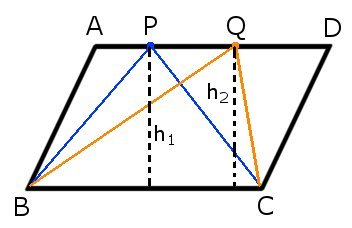
Dato che i due triangoli hanno la stessa base $BC$ e la stessa altezza ($h_1=h_2$), è evidente che le loro aree sono uguali:
$$A_{BPC}=\frac{BC\cdot h_1}{2}=A_{BQC}=\frac{BC\cdot h_2}{2}$$
