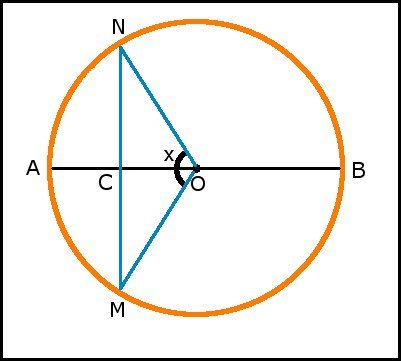
In un settore circolare $AOB$ di raggio $r$ e di ampiezza uguale a $90^\circ$ traccia un raggio $OP$. Considera la proiezione ortogonale $D$ di $P$ sul raggio $OB$ e il punto medio $C$ del raggio $OA$. Determina l'angolo $\widehat{AOP}$ sapendo che è valida la relazione $PC^2+PD^2=\frac{11}{10}r^2$.
DATI DEL PROBLEMA:
PROCEDIMENTO:
Applichiamo il teorema del coseno al triangolo $OCP$:
$\begin{array}{l} PC^2=OP^2+CO^2-2\cdot OP\cdot CO\cdot\cos\widehat{AOP}=r^2+\left(\frac{r}{2}\right)^2-2r\frac{r}{2}\cos\widehat{AOP}=r^2+\frac{r^2}{4}-r^2\cos\widehat{AOP}=\\ =\frac{5}{4}r^2-r^2\cos\widehat{AOP}=r^2\left(\frac{5}{4}-\cos\widehat{AOP}\right)\end{array}$
Poichè $ODP$ è un triangolo rettangolo, si ha:
$PD=OP\sin(90^\circ-\widehat{AOP})=r\cos\widehat{AOP}\quad\quad\Rightarrow\quad\quad PD^2=r^2\cos^2\widehat{AOP}$
Sostituiamo nella relazione $PC^2+PD^2=\frac{11}{10}r^2$ i valori trovati di $PC^2$ e $PD^2$:
$\begin{array}{l} r^2\left(\frac{5}{4}-\cos\widehat{AOP}\right)+r^2\cos\widehat{AOP}=\frac{11}{10}r^2\quad\quad\Rightarrow\quad\quad \cos^2\widehat{AOP}-\cos\widehat{AOP}+\frac{5}{4}-\frac{11}{10}=0\quad\quad\Rightarrow\\ \Rightarrow\quad\quad \cos^2\widehat{AOP}-\cos\widehat{AOP}+\frac{3}{20}=0\quad\quad\Rightarrow\quad\quad 20\cos^2\widehat{AOP}-20\cos\widehat{AOP}+3=0\end{array}$
Trovando le soluzioni di questa equazione nell'incognita $\cos\widehat{AOP}$ abbiamo risolto l'esercizio:
$\cos\widehat{AOP}=\frac{10\pm\sqrt{100-60}}{20}=\frac{5\pm\sqrt{10}}{10}$
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
