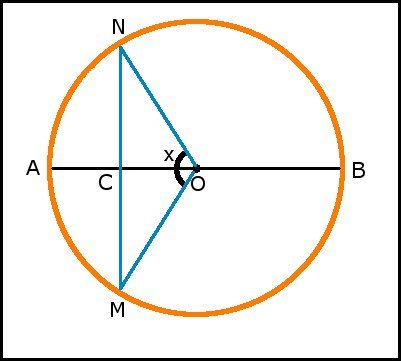
In una circonferenza di centro $O$ e diametro $\overline{AB}=2r$ la corda $MN$ è perpendicolare al diametro e lo divide in due parti che stanno nel rapporto $\frac{7}{3}$. Determina l'ampiezza dell'angolo al centro $\widehat{MON}=2x$
DATI DEL PROBLEMA:
PROCEDIMENTO:
Dal fatto che
$$AC=AB-CB=2r-CB\quad\quad\mbox{e}\quad\quad\frac{CB}{AC}=\frac{7}{3}$$
si ha:
$\begin{array}{l}\frac{CB}{AC}=\frac{CB}{2r-CB}=\frac{7}{3}\quad\quad\Rightarrow\quad\quad CB=\frac{7}{3}(2r-CB)\quad\quad\Rightarrow\quad\quad\\ \Rightarrow\quad\quad CB=\frac{14}{3}r-\frac{7}{3}CB\quad\quad\Rightarrow\quad\quad\left(1+\frac{7}{3}\right)CB=\frac{14}{3}r\quad\quad\Rightarrow\quad\quad\\ \Rightarrow\quad\quad \frac{10}{3}CB=\frac{14}{3}r\quad\quad\Rightarrow\quad\quad 10CB=14r\quad\quad\Rightarrow\quad\quad CB=\frac{14}{10}r=\frac{7}{5}r\end{array}$
Inoltre,
$$OC=CB-r=\frac{7}{5}r-r=\frac{2}{5}r$$
Applicando il teorema al triangolo rettangolo $NCO$ otteniamo:
$OC=ON\cos\frac{\widehat{MON}}{2}\quad\quad\Rightarrow\quad\quad\frac{2}{5}r=r\cos\frac{2x}{2}\quad\quad\Rightarrow\quad\quad\cos x=\frac{2}{5}$
per cui possiamo dire che:
$$x=\arccos\frac{2}{5}\quad\quad\Rightarrow\quad\quad \widehat{MON}=2\arccos\frac{2}{5}$$
