Un triangolo ha per vertici i punti $A=(1,0),\ B=(4,4),\ C=(8,0)$. Trova il suo perimetro e le misure delle sue mediane.
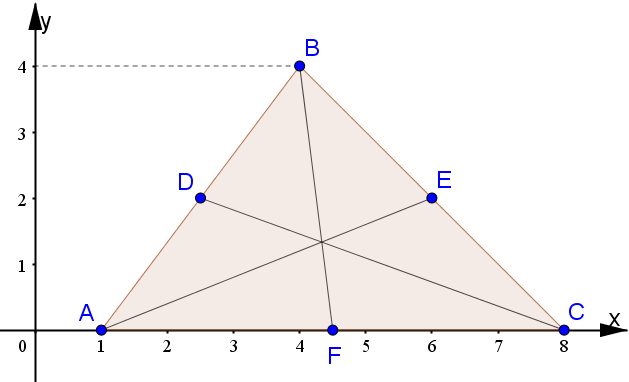
Innanzitutto grafichiamo i vertici e quindi il triangolo.
Banalmente, troviamo le distanze (clicca qui se cono ricordi la formula della distanza tra due punti) AB, BC e CA in modo da calcolare il perimetro: $$\begin{eqnarray*} AB &=& \sqrt{(1-4)^2+(0-4)^2}=\sqrt{9+16}=5\\ BC &=& \sqrt{(4-8)^2+(4-0)^2}=\sqrt{16+16}=\sqrt{2^5}=4\sqrt{2}\\ CA &=& \sqrt{(8-1)^2+(0-0)^2}=\sqrt{49}=7\end{eqnarray*}$$
Il perimetro del triangolo è la somma delle tre distanze calcolate: $$\begin{eqnarray*} P &=& =AB+BC+CA=\\ &=& 5+4\sqrt{2}+7=12+4\sqrt{2}\end{eqnarray*}$$
Ricordando che la mediana è quel segmento che parte dal punto medio di un lato del triangolo e arriva nel vertice opposto, calcoliamo tutti i punti medi dei lati chiamandoli D (medio tra A e B), E(medio tra B e C) ed F(medio tra A e C): $$\begin{eqnarray*} D &=& \left(\frac{1+4}{2},\frac{0+4}{2}\right) =\left(\frac{5}{2},2\right)\\ E &=& \left(\frac{4+8}{2},\frac{4+0}{2}\right) =\left(6,2\right)\\ F &=& \left(\frac{8+1}{2},\frac{0+0}{2}\right) =\left(\frac{9}{2},0\right)\end{eqnarray*}$$
Fatto ciò, possiamo trovare la lunghezza delle mediane DC, EA ed FB mediante la formula della distanza: $$\begin{eqnarray*} DC &=& \sqrt{\left(\frac{5}{2}-8\right)^2+(2-0)^2}=\sqrt{\frac{121}{4}+4}=\sqrt{\frac{137}{4}}\\ EA &=& \sqrt{(1-6)^2+(0-2)^2}=\sqrt{25+4}=\sqrt{29}\\ FB &=& \sqrt{\left(\frac{9}{2}-4\right)^2+(0-4)^2}=\sqrt{\frac{1}{4}+16}=\sqrt{\frac{65}{4}}\end{eqnarray*}$$
Ecco la rappresentazione grafica:
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
