Il piano cartesiano non è altro che uno strumento che ci permette di graficare qualsiasi oggetto della geometria analitica. Prende il nome dal noto filosofo matematico francese Cartesio il quale inventò il sistema di riferimento cartesiano. In due dimensioni tale sistema di coordinate è raffigurato nell'immagine qui in basso.
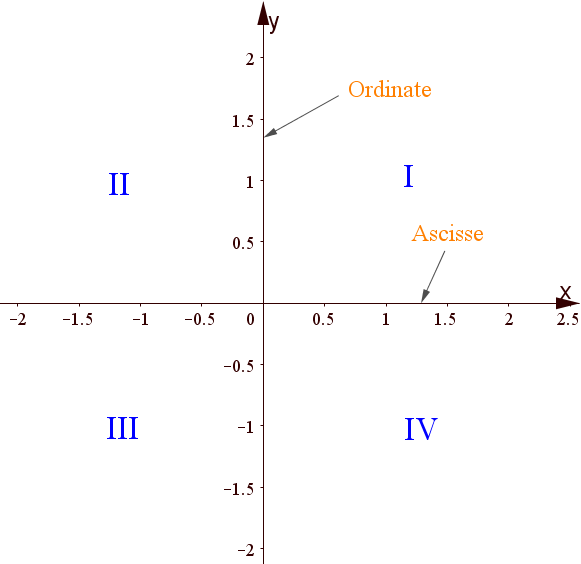
Come si vede dalla figura soprastante, questo consiste in due assi x e y chiamati rispettivamente asse delle ascisse (o asse orizzontale) e asse delle ordinate (o asse verticale). Le frecce degli assi indicano la direzione crescente delle coordinate: valori di x crescenti verso destra e valori di y crescenti verso l'alto.
Il piano cartesiano è diviso in quattro quadranti numerati in senso antiorario da 1 a 4 che si contraddistinguono per il segno di ciascuna coordinata. Ad esempio, il secondo quadrante rappresenta l'insieme di punti del piano che hanno ascisse negative (x < 0) e ordinate positive (y > 0); mentre invece il terzo quadrante ha entrambe ascisse e ordinate negative. Ciò può essere compreso meglio se diamo la definizione di punto nel piano.
Un punto del piano è l'oggetto base della geometria analitica mediante il quale vengono rappresentate le coordinate cartesiane. Un punto, infatti, è una coppia di coordinate x e y (e si indica $(x,y)$) che identificano un'esatta posizione nel piano. Per graficare un punto nel piano bisogna intercettare dapprima la coordinata x sull'asse orizzontale e, da quella posizione, spostarsi verticalmente (verso il basso o verso l'alto) per intercettare la coordinata y esattamente come mostra la figura qui sotto:

Ricorda! Le coordinate di un punto vanno scritte seguendo l'ordine mostrato, ovvero prima la x e poi la y.
Notiamo inoltre la presenza del punto $O(0,0)$, ossia l'origine degli assi.
Formula della distanza tra due punti del piano
Molto spesso, nelle problemi di geometria analitica capita di dover calcolare la distanza tra due punti giacenti sul piano. Allora, dati due punti $P_1=(x_1,y_1)$ e $P_2=(x_2,y_2)$ definiamo distanza tra $P_1$ e $P_2$ e la indichiamo con $d(P_1,P_2)$ oppure $P_1P_2$, la seguente: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{d(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}$$
Tale distanza è nota anche come distanza Euclidea.
Esempio
Troviamo la distanza tra $P_1=(3,-5)$ e $P_2=(5,0)$: $$\begin{eqnarray*} d(P_1,P_2)&=& \sqrt{(3-5)^2+(-5-0)^2}=\\ &=& \sqrt{(-2)^2+(-5)^2} =\sqrt{29}\end{eqnarray*}$$
Verificare se tre punti sono allineati
Utilizzando la formula della distanza Euclidea appena vista, possiamo verificare se tre punti del piano sono allineati, ossia giacciono tutti sulla stessa linea retta. Infatti, supponiamo di avere tre punti A,B e C come mostrato qui sotto:
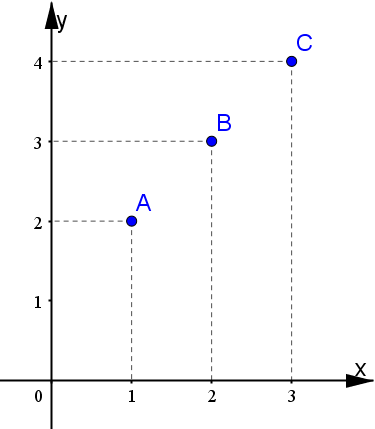
per verificare se questi sono allineati o no, dobbiamo verificare la seguente uguaglianza: $$d(A,C)=d(A,B)+d(B,C)\ (\large\star)$$
Esempio
Dire se i punti $A=(1,2),\ B=(2,3),\ C=(3,4)$ sono allineati:
Calcoliamo le tre distanze: $$\begin{eqnarray*} d(A,C)&=& \sqrt{(3-1)^2+(4-2)^2}=\sqrt{8}=2\sqrt{2}\\ d(A,B &=& \sqrt{(2-1)^2+(3-2)^2}=\sqrt{2}\\ d(B,C)&=& \sqrt{(3-2)^2+(4-3)^2}=\sqrt{2}\end{eqnarray*}$$
Otteniamo che la $(\large\star)$ è verificata: $$2\sqrt{2}=\sqrt{2}+\sqrt{2}$$ perciò i punti A,B e C sono allineati.
Osserviamo che tale concetto deriva da una proprietà della distanza chiamata proprietà triangolare, la quale afferma che dati 3 punti A,B e C risulta sempre: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{d(A,C)\leq d(A,B)+d(B,C)}$$
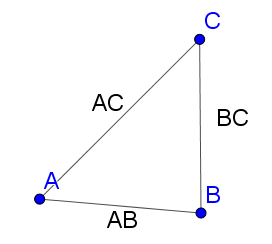
L'uguaglianza si ha proprio nel caso in cui i punti sono allineati.
Formula del punto medio tra due punti
Il punto medio tra due punti è quello che sta a metà strada tra i due.
Considerando sempre i due punti $P_1$ e $P_2$, il punto medio M si calcola così: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{M=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)}$$
Esempio
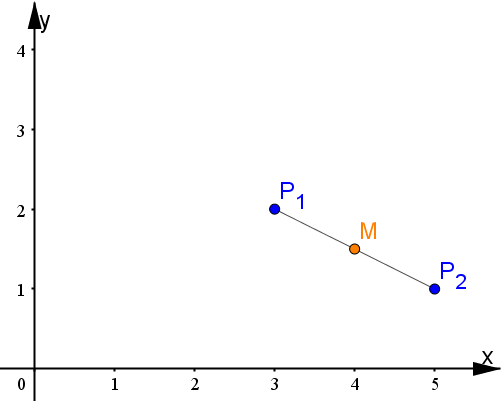
Calcolare il punto medio tra $P_1=(3,2)$ e $P_2=(5,1)$.
Applicando la formula soprascritta, otteniamo: $$M=\left(\frac{3+5}{2},\frac{2+1}{2}\right)=\left(4,\frac{3}{2}\right)$$