Se hai appena iniziato a studiare la geometria analitica, ti sarai già imbattuto in esercizi e problemi che coinvolgono gli aspetti grafici e algebrici (equazioni) delle rette.
Qui di seguito puoi consultare tanti esercizi risolti sulle rette nel piano in modo da comprendere le equazioni e le formule delle rette viste nella teoria.
Tra le rette di equazione $kx+(k-1)y+2=0$ individua quella parallela alla retta $x+3y+5=0$.
Il generico coefficiente angolare (vedi la formula nel caso di equazione in forma implicita) del fascio di rette $kx+(k-1)y+2=0$ è: $$m=-\frac{a}{b}=-\frac{k}{k-1}$$
Il coefficiente angolare della retta data è invece $$m'=-\frac{1}{3}$$
Affichè la retta cercata sia parallela a quella data, è necessario imporre che il generico coefficiente angolare del fascio di rette sia uguale al coefficiente angolare della retta data (condizione di parallelismo tra rette): $$m=m'\ \Leftrightarrow\ -\frac{k}{k-1}=-\frac{1}{3}$$
Risolvendo quest'ultima e tenendo conto della condizione di esistenza $k-1\neq 0\ \Rightarrow\ k\neq 1$, otteniamo: $$\begin{array}{l} \frac{k}{k-1}=\frac{1}{3}\\ \frac{3k}{3(k-1)}=\frac{k-1}{3(k-1)}\\ 3k=k-1\\ k=-\frac{1}{2} \end{array}$$
Tale $k$ è quel valore che se sostituito nell'equazione del fascio di rette data, ci ritorna l'equazione della retta richiesta: $$\begin{array}{l} kx+(k-1)y+2=0\\ -\frac{1}{2}x+(-\frac{1}{2}-1)y+2=0\\ -\frac{1}{2}x-\frac{3}{2}y+2=0\\ -x-3y+4=0\\ x+3y-4=0 \end{array}$$
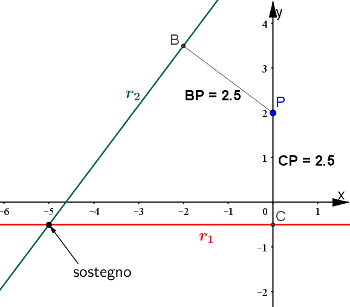
Le due rette $x-2y+4=0$ e $2x+2y+11=0$ individuano un fascio proprio il cui sostegno è il loro punto di intersezione. Tra le rette di questo fascio trova quelle la cui distanza dal punto $P=(0,2)$ è $5/2$.
Come spiegato in questa lezione, il fascio di rette generato dalle due rette date è: $$A(x-2y+4)+B(2x+2y+11)=0$$
Semplifichiamo tale equazione riscrivendola al solo variare di un parametro $k=B/A$: $$\begin{array}{l} (x-2y+4)+k(2x+2y+11)=0\\ (1+2k)x+(-2-2k)y+4+11k=0\ \large\star \end{array}$$
Utilizzando la formula della distanza punto-retta (punto $P=(0,2)$ e retta $ax+by+c=0$ da trovare) e imponendo che questa sia pari a $5/2$, otteniamo $$\begin{array}{l} \frac{|a\cdot 0+b\cdot 2+c|}{\sqrt{a^2+b^2}}=\frac{5}{2}\\ \frac{|2b+c|}{\sqrt{a^2+b^2}}=\frac{5}{2}\\ |4b+2c|=5\sqrt{a^2+b^2}\\ \left(\frac{4b}{5}+\frac{2c}{5}\right)^2=a^2+b^2 \end{array}$$
In quest'ultima equazione, sostituiamo i valori di $a$, $b$ e $c$ rispettivamente con i coefficienti del fascio $\large\star$ $(1+2k)$, $(-2-2k)$ e $4+11k$: $$\begin{array}{l} \left(\frac{-8+8k}{5}+\frac{8+22k}{5}\right)^2=(1+2k)^2+(-2+2k)^2\\ (\cancel{-8}+8k\cancel{+8}+22k)^2=(5+10k)^2+(-10+19k)^2\\ 900k^2=25+100k+100k^2+100-200k+100k^2\\ 700k^2+100k-125=0 \end{array}$$
Risolvendo l'equazione di secondo grado in k otteniamo le radici $k=\frac{5}{14}$ e $k=-\frac{1}{2}$.
Tali radici sono quei valori di k che se sostituiti nell'equazione del fascio $\large\star$, vengono fuori le rette con le caratteristiche cercate. In particolare, per $k=-\frac{1}{2}$, otteniamo: $$\begin{array}{l} \bigg[ 1+2\left(-\frac{1}{2}\right)\bigg ]x+\bigg [-2-2\left(-\frac{1}{2}\right)\bigg ]y+4+11\left(-\frac{1}{2}\right)=0\\ -3y+4-\frac{11}{2}=0\\ r_1:\ y=-\frac{1}{2} \end{array}$$
Per $k=\frac{5}{14}$ invece si ha: $$\begin{array}{l} \left(1+2\cdot\frac{5}{14}\right)x+\left(-2-2\cdot\frac{5}{14}\right)y+4+11\cdot \frac{5}{14}=0\\ \left(1+\frac{5}{7}\right)x+\left(-2+\frac{5}{7}\right)y+4+\frac{55}{14}=0\\ r_2:\ 8x-6y+37=0 \end{array}$$
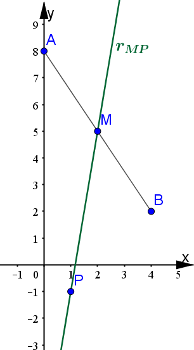
Data l'equazione del fascio di rette $kx+(2k-1)y+k-1=0$ determina il sostegno P. Determina poi, tra le rette del fascio, quella che interseca il segmento di estremi $A=(0,8)$ e $B=(4,2)$ nel suo punto medio e quella la cui distanza dall'origine del sistema di riferimento è $\sqrt{34}/17$.
Il sostegno di un fascio proprio di rette si trova come punto di intersezione tra due rette qualsiasi ad esso appartenenti. Possiamo ricavare tali rette sostituendo dei valori arbitrari nell'equazione del fascio: $$\begin{array}{l} k=0\ \Rightarrow\ y=-1\\ k=1\ \Rightarrow\ x+y=0 \end{array}$$
Facendo il sistema tra queste due rette, otteniamo il sostegno di coordinate $P=(1,-1)$.
Adesso calcoliamo le coordinate del punto medio del segmento: $$M=\left(\frac{0+4}{2},\frac{8+2}{2}\right)=(2,5)$$
La retta del fascio che interseca il segmento in $M$ è la retta passante per il sostegno $P$ ed $M$ stesso (equazione retta passante per due punti): $$\begin{array}{l} \frac{x-2}{1-2}=\frac{y-5}{-1-5}\\ -x+2=\frac{-y+5}{6}\\ r_{MP}:\ 6x-y-7=0\end{array}$$
Adesso determiniamo le equazioni delle altre rette del fascio che distano $\sqrt{34}/17$ dall'origine degli assi $(0,0)$ esattamente come fatto nel problema 2. Imponiamo dapprima che la distanza dal fascio sia $\frac{\sqrt{34}}{17}$
$$\begin{array}{l} \frac{|k-1|}{\sqrt{k^2+4k^2-4k+1}}=\frac{\sqrt{34}}{17}\\ 17|k-1|=\sqrt{34}\sqrt{5k^2-4k+1}\\ [17(k-1)]^2=170k^2-136k+34\\ 7k^2-26k+15=0 \end{array}$$
Le radici dell'ultima equazione sono: $k=3$ e $k=\frac{5}{7}$. Sostituendole nell'equazione del fascio, troviamo le rette richieste.
Per $k=3$ otteniamo $$3x+5y+2$$ mentre per $k=\frac{5}{7}$ abbiamo $$5x+3y-2=0$$
Dato il fascio di rette $y=2x+k$, trovare quelle rette che assieme agli assi cartesiani formano un triangolo di area 5.
Notiamo che si tratta di un fascio di rette improprio formato da infinite (al variare di $k$) rette parallele con coefficiente angolare pari a 2.
Troviamo le intersezioni del fascio di rette con gli assi cartesiani. Intersecando con l'asse y ($x=0$) otteniamo: $$\begin{cases} x=0\\ y=2x+k\ \Rightarrow\ y=k \end{cases}$$ ossia il punto $A=(0,k)$.
Intersecando con l'asse y ($x=0$) si ha: $$\begin{cases} y=0\\ y=2x+k\ \Rightarrow\ x=-\frac{k}{2} \end{cases}$$ e quindi il punto $B=\left(-\frac{k}{2},0\right)$.
Osservando il grafico sottostante, notiamo che i segmenti OA e OB rappresentano base e altezza del triangolo che si viene a formare. Per essere più precisi, rimangono individuati anche altri due punti $A'$ e $B'$, ossia i corrispondenti vertici del triangolo che si forma simmetricamente all'asse y.
Calcoliamo la misura dei cateti: $$\begin{eqnarray*} \overline{OA}&=& \overline{OA'}=|k|\\ \overline{OB}&=& \overline{OB'}=\bigg |-\frac{k}{2}\bigg | \end{eqnarray*}$$
Ricordando che l'area del triangolo rettangolo uguagliata a 5 è base per altezza diviso 2, si ha: $$\begin{array}{l} \frac{\overline{OA}\cdot \overline{OB}}{2}=5\\ \frac{|k|\cdot |-\frac{k}{2}\bigg |}{2}=5\\ \frac{1}{4}k^2=5\\ k^2=20\\ k=\pm\sqrt{20}\end{array}$$
Sostituendo i valori di k trovati nell'equazione del fascio $y=2x+k$, troviamo le rette cercate: $$y=2x+\sqrt{20},\quad y=2x-\sqrt{20}$$
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
