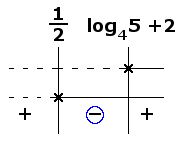Calcolo intervallo di convergenza e somma di una serie di potenza

Calcoliamo come prima cosa il raggio di convergenza della serie, applicando il criterio di D'Alembert e cioè calcolando il seguente limite per $n \rightarrow +\infty$

\begin{eqnarray*} \left| \frac{a_{n+1}}{a_n} \right| &=& \frac{|1 + (-1)^{n} \ 2^{n+1}|}{|1 + (-1)^{n-1} \ 2^n|} = \frac{|1 + (-1)^{n} \ 2^{n+1}|}{|1 - (-1)^{n} \ 2^n|} = \left| \frac{1 + (-1)^{n} \ 2^{n+1}}{1 - (-1)^{n} \ 2^n} \ \frac{1 + (-1)^{n} \ 2^n}{1 + (-1)^{n} \ 2^n} \right| =\\ &=& \frac{1+(-1)^n 2^n+ (-1)^n 2^{n+1}+2^{2n+1}}{1-2^{2n}} = \frac{|1+(-1)^n (2^n +2^{n+1}) + 2^{2n+1}|}{2^{2n} -1} = \\ &=& \frac{1}{2^{2n}-1} + \frac{2^n +2^{n+1}}{2^{2n} -1} + \frac{2^{2n+1}}{2^{2n} -1} = \frac{1}{2^{2n}-1} + \frac{2^n \ ( 1 + 2 )}{2^n \ (2^n - \frac{1}{2^n} )} + \frac{2^{2n} \ (2)}{2^{2n} \ ( 1 - \frac{1}{2^{2n}})} =\\ &=& \frac{1}{2^{2n}-1} + \frac{3}{2^n - \frac{1}{2^n}} + \frac{2}{1- \frac{1}{2^{2n}}} \rightarrow 2 \end{eqnarray*}

visto che le prime due frazioni, nel limite per $n \rightarrow +\infty$ vanno a zero e l'ultima tende a $2$.

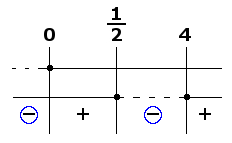
Il raggio di convergenza è quindi $R = \frac{1}{2}$. Allora, per il teorema di convergenza per le serie di potenze, la serie converge puntualmente in ogni $x : |x-x_0|< R$, ovvero

$$I_c\ = \ ]-\frac{1}{2},\ \frac{1}{2}[$$

Lo stesso teorema garantisce che la serie di potenze converge uniformemente in ogni intervallo chiuso e limitato del tipo $[x_0-k, \ x_0+k]$, con $ k\in ]0,\ R[ $. Quindi nel nostro caso, la serie converge puntualmente in $I_c$ ed uniformemente in ogni intervallo $[-k,\ k],\ k \in ]0, \ \frac{1}{2}[$.

Per concludere l'esercizio rimane da calcolare la somma della serie. Come prima cosa divido la serie come somma di due serie, precisamente:

$$\sum\limits_{n=1}^{+\infty} [1 + (-1)^{n-1} \ 2^n] \ x^{n-1} = \sum\limits_{n=1}^{+\infty} x^{n-1} + \sum\limits_{n=1}^{+\infty} (-1)^{n-1} \ 2^n \ x^{n-1}$$

La prima serie è una serie geometrica che ha come somma $\frac{1}{x-1}$ per $|x|<1$. Ricordando il valore di $I_c$ non abbiamo quindi problemi.

La seconda serie la scrivo invece come

$$\sum\limits_{n=1}^{+\infty} (-1)^{n-1} \ 2^n \ x^{n-1} = 2 \ \sum\limits_{n=1}^{+\infty} (-1)^{n-1}\ (2 x)^{n-1} = 2 \frac{1}{1+2x}, \quad x\neq \frac{1}{2}$$

ricordando per l'ultima uguaglianza che $\sum\limits_{n=0}^{+\infty} (-1)^{n} t^n = \frac{1}{1+t}$. L'esercizio è così concluso.

Calcoliamo come prima cosa il raggio di convergenza della serie, applicando il criterio di D'Alambert e cioè calcolando il seguente limite per $n \rightarrow +\infty$

$$\left| \frac{a_{n+1}}{a_n} \right| = \left| \frac{2n (2n-1)}{2(n+1)(2(n+1) -1)} \right| = \left| \frac{2n (2n-1)}{(2n+2)(2n+1)} \right| \longrightarrow 1 $$

Per il teorema di convergenza per le serie di potenze, poichè $R=1$, la serie converge puntualmente in ogni $x : |x-x_0|< R$, ovvero

$$I_c\ = \ ]-1,\ 1[$$

Lo stesso teorema garantisce che la serie di potenze converge uniformemente in ogni intervallo chiuso e limitato del tipo $[x_0-k, \ x_0+k]$, con $ k\in ]0,\ R[ $.

Quindi nel nostro caso, la serie converge puntualmente in $I_c$ ed uniformemente in ogni intervallo $[-k,\ k],\ k \in ]0, \ 1[$.

Vediamo il comportamento della serie agli estremi. Per $x = \pm 1$ la serie diventa la seguente serie a segni alterni:

$$\sum\limits_{n=1}^{+\infty} (-1)^n \frac{1}{2n(2n-1)}$$

Notiamo che sono verificate tutte le ipotesi del Teorema di Leibiniz, ovvero

$$a_n = \frac{1}{2n(2n-1)} \quad \mbox{ monotona descrescente e} $$ $$\frac{1}{2n(2n-1)} \rightarrow 0 \quad \mbox{per} \quad n \rightarrow +\infty$$

Quindi per il criterio di Leibiniz la serie converge anche agli estremi e l'intervallo di convergenza diventa quindi $I_c = [-1, \ 1]$.

Per concludere l'esercizio rimane da calcolare la somma della serie. A questo scopo, applichiamo il Teorema di derivazione per serie di potenze.

Sia $f(x) = \sum\limits_{n=1}^{+\infty} (-1)^n \frac{x^{2n}}{2n(2n-1)}$. Calcoliamo allora la derivata di $f(x)$:

\begin{eqnarray*} f'(x) &=& \left[ \sum\limits_{n=1}^{+\infty} (-1)^n \frac{x^{2n}}{2n(2n-1)} \right]' = \sum\limits_{n=1}^{+\infty} (-1)^n \frac{ 2n \ x^{2n-1}}{2n(2n-1)} = \\ &=& \sum\limits_{n=1}^{+\infty} (-1)^n \frac{x^{2n-1}}{2n-1} = -x + \frac{x^3}{3} - \frac{x^5}{5} + \frac{x^7}{7} + \cdots = -\arctan x \Rightarrow \end{eqnarray*} \begin{eqnarray*} f(x) &=& \int -\arctan x \ dx = -x \arctan x + \int \frac{x}{1+x^2} \ dx = -x \arctan x + \frac{1}{2} \log (1+x^2) + c \end{eqnarray*}

Per trovare la costante di integrazione $c$, valuto l'espressione di $f(0)$. Trovo quindi $0= f(0) = c$.

In definitiva $f(x) = -x \arctan x + \frac{1}{2} \log (1+x^2)$ e l'esercizio è così concluso.