Studiare la funzione con esponenziale e valore assoluto e tracciarne il grafico $$f(x)=(|x+1|-2)e^{-(x^2-1)}$$
Campo di esistenza
La funzione è definita e continua in tutto $\mathbb{R}$.
Positività
Essendo l'esponenziale definito positivo in tutto il suo dominio, basta studiare il segno della sola parentesi, ossia: $$\begin{array}{l} |x+1|-2 > 0\\ |x+1| > 2\\ x+1 < -2\ \vee\ x+1 > 2\\ x < -3\ \vee\ x > 1\end{array}$$
Intersezioni con gli assi
Dallo studio del segno ricaviamo che $x=-3$ e $x=1$ sono intersezioni con l'asse x. Imponendo invece $x=0$ nell'espressione della funzione, otteniamo le intersezioni con l'asse y: $$f(0)=(|0+1|-2)e^{-(0^2-1)}=-e$$
Limiti e asintoti
Gli unici limiti da calcolare sono quelli a $\pm\infty$. Inoltre, osserviamo che per $x\rightarrow +\infty$ la quantità x+1 è positiva, dunque è lecito togliere il valore assoluto:
$$\lim\limits_{x\rightarrow +\infty}(x+1-2)e^{-(x^2-1)}=\lim\limits_{x\rightarrow +\infty}(x-1)e^{-(x^2-1)}=[+\infty\cdot 0]$$
Per risolvere la forma determinata possiamo applicare il teorema di De L'Hopital, infatti: $$\begin{array}{l} (x-1)e^{-(x^2-1)}=\\ =\frac{x-1}{e^{(x^2-1)}}\overset{x\rightarrow +\infty}{\longrightarrow}\frac{+\infty}{+\infty}\end{array}$$ Derivando rispetto $x$ numeratore e denominatore dell'ultima frazione otteniamo: $$\frac{1}{e^{(x^2-1)}\cdot 2x}\overset{x\rightarrow -\infty}{\longrightarrow}\frac{1}{+\infty}=0$$
Si ha dunque che $y=0$ è un asintoto orizzontale destro.
Invece per $x\rightarrow -\infty$ la quantità x+1 è negativa, dunque è eliminiamo il valore assoluto aggiungendo un segno meno:
$$\lim\limits_{x\rightarrow -\infty}(-x-1-2)e^{-(x^2-1)}=\lim\limits_{x\rightarrow -\infty}(-x-3)e^{-(x^2-1)}=[+\infty\cdot 0]$$
Applicando nuovamente il teorema di De L'Hopital: $$\begin{array}{l} (-x-3)e^{-(x^2-1)}=\\ =\frac{-x-3}{e^{(x^2-1)}}\overset{x\rightarrow -\infty}{\longrightarrow}\frac{+\infty}{+\infty}\end{array}$$ $$\frac{-1}{e^{(x^2-1)}\cdot 2x}\overset{x\rightarrow -\infty}{\longrightarrow}\frac{1}{-\infty}=0$$
Si ha dunque che $y=0$ è pure asintoto orizzontale sinistro, per cui un asintot orizzontale completo.
Essendoci un asintoto orizzontale completo, possiamo affermare che non esistono asintoti obliqui.
Derivata prima
Poichè la derivata di una funzione contenente il valore assoluto cambia al variare del segno assunto, riscriviamo la $f(x)$ distinguendo i casi $x+1\geq 0$ e $x+1 < 0$, ossia rispettivamente $x\geq -1$ e $x < -1$. $$f(x)=\begin{cases} (x-1)e^{-(x^2-1)} & \mbox{se } x\geq -1\\ (-x-3)e^{-(x^2-1)} & \mbox{se } x < -1\end{cases}$$
Derivando la prima legge per $x\geq -1$ otteniamo: $$\begin{eqnarray*} f'(x)&=&e^{-(x^2-1)}+(x-1)e^{-(x^2-1)}(-2x)=\\ &=&e^{-(x^2-1)}[1-2x(x-1)]=\\ &=&e^{-(x^2-1)}(1-2x^2+2x)\end{eqnarray*}$$
Studiare il segno di quest'ultima equivale a studiare il segno dell'ultima parentesi $(-2x^2+2x+1)>0$, ossia $(2x^2-2x-1)>0$: $$\begin{array}{l} \frac{\Delta}{4}=1+2=3\\ x=\frac{1\pm\sqrt{3}}{2}\end{array}$$ da cui si ottengono le soluzioni della disequazione di partenza: $\frac{1-\sqrt{3}}{2} < x < \frac{1+\sqrt{3}}{2}$. Il grafico del segno è il seguente: 
Notiamo un punto min per $x=\frac{1-\sqrt{3}}{2}$ e un punto max1 per $x=\frac{1+\sqrt{3}}{2}$
Derivando la seconda legge per $x < -1$ otteniamo: $$\begin{eqnarray*} f'(x)&=&-e^{-(x^2-1)}+(-x-3)e^{-(x^2-1)}(-2x)=\\ &=&e^{-(x^2-1)}[-1+2x(x+3)]=\\ &=&e^{-(x^2-1)}(-1+2x^2+6x)\end{eqnarray*}$$
Studiare il segno di quest'ultima equivale a studiare il segno dell'ultima parentesi $(2x^2+6x-1)>0$: $$\begin{array}{l} \frac{\Delta}{4}=9+2=11\\ x=\frac{-3\pm\sqrt{11}}{2}\end{array}$$ da cui si ottengono le soluzioni della disequazione di partenza: $x < \frac{-3-\sqrt{11}}{2}\ \vee\ x > \frac{-3+\sqrt{11}}{2}$. Il grafico del segno, tenendo conto del fatto che $x < -1$ è il seguente: 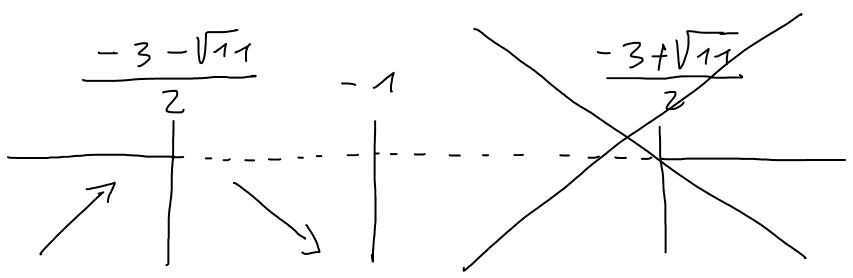
È chiaro dal grafico che otteniamo un altro punto di massimo per $x=\frac{-3-\sqrt{11}}{2}$.
Derivata seconda
Consideriamo la funzione derivata prima ottenuta al passo precedente $$f'(x)=\begin{cases} e^{-(x^2-1)}(1-2x^2+2x) & \mbox{se } x\geq -1\\ e^{-(x^2-1)}(-1+2x^2+6x) & \mbox{se } x < -1\end{cases}$$ e deriviamole rispettavemente ancora una volta.
Per $x\geq -1$ si ha: $$\begin{eqnarray*} f^{''}(x)&=& e^{-(x^2-1)}(-2x)(1-2x^2+2x)+e^{-(x^2-1)}(-4x+2)=\\ &=&e^{-(x^2-1)}[(-2x)(1-2x^2+2x)-4x+2]=\\ &=&e^{-(x^2-1)}(-2x+4x^3-4x^2-4x+2)=\\ &=&2e^{-(x^2-1)}(2x^3-2x^2-3x+1)\end{eqnarray*}$$
Per $x > -1$ si ha: $$\begin{eqnarray*} f^{''}(x)&=& e^{-(x^2-1)}(-2x)(-1+2x^2+6x)+e^{-(x^2-1)}(4x+6)=\\ &=&e^{-(x^2-1)}[(-2x)(-1+2x^2+6x)+4x+6]=\\ &=&e^{-(x^2-1)}(2x-4x^3-12x^2-4x+6)=\\ &=&e^{-(x^2-1)}(-4x^3-12x^2-2x+6)=\\ &=&2e^{-(x^2-1)}(-2x^3-6x^2-x+3)\end{eqnarray*}$$
Come succede spesso, studiare il segno della derivata seconda non è immediato. Essendo questo il nostro caso, ci limitiamo a tracciare un grafico qualitativo (probabile) considerando le informazioni trovate nei punti precedenti. 
Qui sotto invece, una vista più da vicino nei dintorni del punto max2. 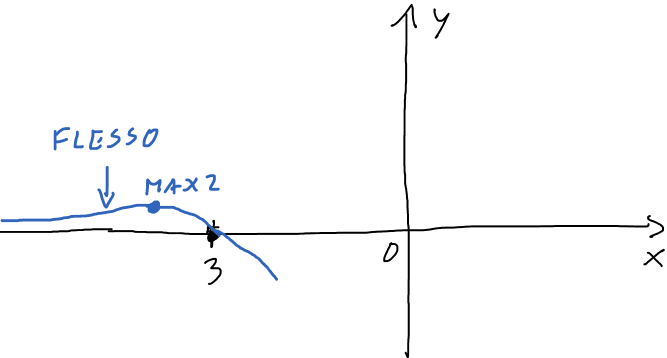
Altri esercizi di matematica

Equazioni numeriche fratte risolte

Esercizi svolti con il criterio del rapporto
Disequazioni con radici e valore assoluto risolte

Domini o campi di esistenza di funzioni risolti
Esercizi sulla scomposizione riconducibile a prodotti notevoli
Disequazioni logaritmiche risolte

Calcolo coefficienti della funzione omografica

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare