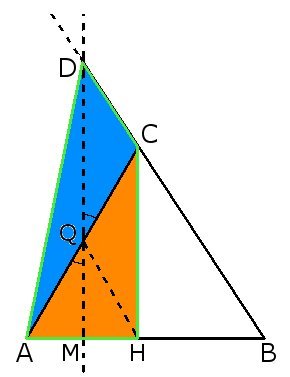
In un parallelogramma ABCD, si considera il punto P sulla diagonale AC. Dimostrare che i 4 triangoli che si formano sono a due a due equivalenti.
Il triangolo DPC è equivalente al triangolo BPC poichè hanno a comune la stessa base PC e uguale altezza ($DH=BK$). Grazie a ciò, poichè la diagonale AC divide il parallelogramma in due triangoli equivalenti ($A_{ADC}=A_{ABC}$), anche i triangoli APD e APB risultano avere la stessa area. Tale risultato può essere ottenuto facilmente ragionando per differenza:
$$A_{APD}=A_{ADC}-A_{DPC}=A_{ABC}-A_{BPC}=A_{APB}$$
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
