$$\int\!\!\!\! \int _{D} \left( xy + \frac{1}{1+y^2}\right)\ dx\ dy$$ con D porzione di piano delimitato da rette.
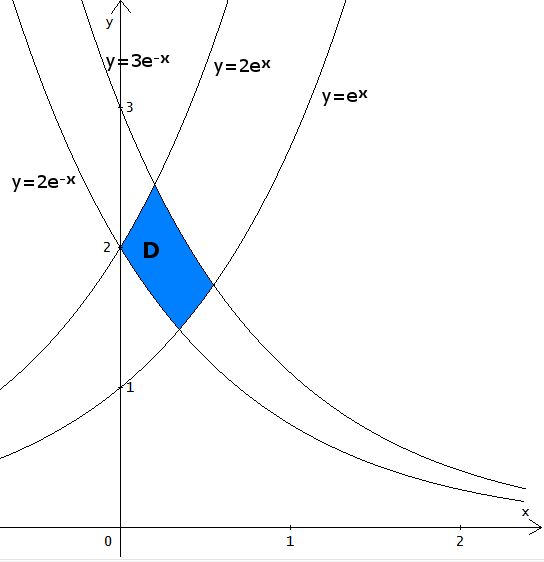
$$\int\!\!\!\! \int _{D} \left( xy + \frac{1}{1+y^2}\right)\ dx\ dy$$ dove D è l'insieme raffigurato nella seguente figura: 
Dalla rappresentazione del dominio $D$ vedo che esso è compreso tra le rette $y=2x \ $ e $y=x-1 \ $ e poi tra $y=-x+3 \ $ e $y=0 \ $. Allora è conveniente dividere il dominio in due sottodomini $D_1$ e $D_2$ normali rispetto all'asse $\overrightarrow{x}$ .
$$ D_{1} = \left \{ (x,y) \in \mathbb{R}^2 : \ 0 \le x \le 1, \ 0 \le y \le 2x \right \}$$ e $$D_{2} = \left \{ (x,y) \in \mathbb{R}^2 : \ 1 \le x \le 2, \ x-1 \le y \le -x+3 \right \}$$
I due domini sono quelli evidenziati in rosso e blu nella figura sottostante.
L'integrale di partenza sarà allora la somma degli integrali sui due domini:
$$\begin{eqnarray*} \int\!\!\!\! \int _{D} \left( xy + \frac{1}{1+y^2} \right)\ dx\ dy & = & \int\!\!\!\! \int _{D_1} \left( xy + \frac{1}{1+y^2}\right)\ dx\ dy + \int\!\!\!\! \int _{D_2} \left( xy + \frac{1}{1+y^2}\right)\ dx\ dy =\\ & = & \int _{0}^{1} \left[ \int_{0}^{2x} \left( xy + \frac{1}{1+y^2}\right)\ dy \right] \ dx + \int _{1}^{2} \left[ \int_{x-1}^{-x+3} \left( xy + \frac{1}{1+y^2} \right) \ dy \right] \ dx =\\ & = & \int _{0}^{1} \left[ \frac{x}{2} \ \left[y^2 \right]_{0}^{2x} + \left[\arctan y \right]_{0}^{2x} \right] \ dx + \int _{1}^{2} \left[ \frac{x}{2} \ \left[y^2 \right]_{x-1}^{-x+3} + \left[\arctan y \right]_{x-1}^{-x+3} \right] \ dx = \\ & = & \int _{0}^{1} \left[ \frac{x}{2} \ 4x^2 + \arctan 2x \right] \ dx + \\ & + & \int _{1}^{2} \left[ \frac{x}{2} \ \left( (-x+3)^2 - (x-1)^2 \right) + \arctan(-x+3) - \arctan(x-1) \right] \ dx = \\ & = & \int _{0}^{1} 2 x^3 \ dx + \int _{0}^{1} \arctan 2x \ dx + \int _{1}^{2} \left[ \frac{x}{2} \ \left( x^2 -6x + 9 - x^2 + 2x -1 \right) \right] \ dx + \\ & + & \int _{1}^{2} \arctan (-x+3) \ dx - \int _{1}^{2} \arctan (x-1) \ dx = \\ & = & \frac{2}{4} \left[ x^4 \right]_{0}^{1} + \left[ x \ \arctan 2x \right]_{0}^{1} - \int _{0}^{1} \frac{2x}{1+ (2x)^2} \ dx + \int _{1}^{2} \left[ \frac{x}{2} \ (-4x + 8) \right] \ dx + \\ & + & \left[ x \ \arctan (-x+3)\right]_{1}^{2} - \int_{1}^{2} \frac{-x}{1+ (-x+3)^2} \ dx - \left[ x \ \arctan( x-1) \right]_{1}^{2} +\\ & + & \int_{1}^{2} \frac{x}{1+(x-1)^2} \ dx \end{eqnarray*}$$
Osserviamo che gli integrali con l' $\arctan$ sono stati svolti per parti. Adesso risolviamo separatamente gli integrali che rimangono nell'ultima espressione. Si ha:
$$\begin{eqnarray*}& \int_{0}^{1} &\frac{2x}{1+(2x)^2} \ dx =\\ &=&\frac{1}{4} \int_{0}^{1} \frac{4 \cdot 2x}{4 x^2 +1} \ dx =\\ &=& \left[ \frac{1}{4} \ln (4x^2 + 1)\right]_{0}^{1}=\\ &=&\frac{1}{4} \ln (5)\end{eqnarray*}$$
$$\begin{eqnarray*}& \int_{1}^{2} &\frac{-x}{1+(-x+3)^2} \ dx = \\& = & \int_{1}^{2} \frac{-x+3-3}{1+(-x+3)^2} \ dx =\\ &=& -\frac{1}{2} \int_{1}^{2} \frac{-2(-x+3)}{1+(-x+3)^2} \ dx + 3 \int_{1}^{2} \frac{-1}{1+(-x+3)^2} \ dx = \\ &=& -\frac{1}{2} \left[ \ln \left( 1+ (-x+3)^2 \right)\right]_{1}^{2} + 3\left( \frac{\pi}{4} - \arctan 2 \right)=\\ &=& -\frac{1}{2} \ln 2 + \frac{1}{2} \ln 5 + \frac{3 \pi}{4} -3 \arctan 2. \end{eqnarray*}$$
$$ \begin{eqnarray*}& \int_{1}^{2}& \frac{x}{1+(x-1)^2} \ dx= \\& = & \int_{1}^{2} \frac{x-1+1}{1+(x-1)^2} \ dx \\& = & \int_{1}^{2} \frac{x-1}{1+(x-1)^2} \ dx + \int_{1}^{2} \frac{1}{1+(x-1)^2} \ dx= \\ &=& \frac{1}{2} \left[ \ln [1+(x-1)^2]\right]_{1}^{2} + \left[ \arctan(x-1)\right]_{1}^{2}\\& = & \frac{1}{2} \ln2 + \frac{\pi}{4} \end{eqnarray*}$$
Adesso, mettendo insieme questi integrali con i precedenti e svolgendo tutti i calcoli otteniamo:
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
