Disequazioni con radici e valore assoluto risolte

La prima cosa da fare quando ho di fronte una disequazione del genere è il campo di esistenza. In questo caso è necessario porre il radicando maggiore o uguale a zero per garantire l'esistenza della radice:

$-x^2+2x+3\ge 0\quad\Rightarrow\quad x^2-2x-3\le 0\quad\Rightarrow\quad -1\le x\le 3$

Possiamo adesso iniziare a svolgere la disequazione data. Essendo una disequazione fratta, poniamo sia numeratore che denominatore maggiore di zero e risolviamo tali disequazioni separatamente:

1. $|-x+1|-1 >0$
2. $-2x+\sqrt{-x^2+2x+3} > 0$

Iniziamo con il risolvere la 1) osservando che si tratta di una disequazione con valore assoluto.

$\begin{array}{l} |-x+1|-1 >0\quad\quad\Rightarrow\quad\quad |-x+1| > 1\quad\quad\Rightarrow\quad\quad -x+1 < -1\ \vee\ -x+1 > 1\quad\quad\Rightarrow\\ \Rightarrow\quad\quad x > 2\ \vee\ x < 0\quad\quad\Rightarrow\quad\quad x < 0\ \vee\ x > 2\end{array}$

Facciamo in modo che tale soluzione appartenga al campo di esistenza $-1\le x\le 3$ risolvendo il seguente sistema:

$$\begin{cases} x < 0\ \vee\ x > 2\\ -1\le x\le 3\end{cases}$$

Banalmente, la soluzione del sistema è $-1\le x < 0\ \vee\ 2 < x \le 3$.

Risolviamo adesso la 2).

$-2x+\sqrt{-x^2+2x+3} > 0 \quad\quad\Rightarrow\quad\quad \sqrt{-x^2+2x+3} > 2x$

Impostiamo i due sistemi per risolvere la precedente disequazione irrazionale:

$(a)\begin{cases} -x^2+2x+3\ge 0\\ 2x\ge 0\\ -x^2+2x+3 > 4x^2\end{cases}\quad \vee\quad (b)\begin{cases} -x^2+2x+3\ge 0\\ 2x < 0\end{cases}$

Risolviamo dapprima il sistema (a):

$\begin{cases} -x^2+2x+3\ge 0\\ 2x\ge 0\\ -x^2+2x+3 > 4x^2\end{cases}\quad\Rightarrow\quad\begin{cases} x^2-2x-3\le 0\\ x\ge 0\\ 5x^2-2x-3 < 0\end{cases}\quad\Rightarrow\quad\begin{cases} -1\le x\le 3\\ x\ge 0\\ -\frac{3}{5} < x < 1\end{cases}$

Dal grafico sottostante è evidente che la soluzione del sistema (a) è $0\le x < 1$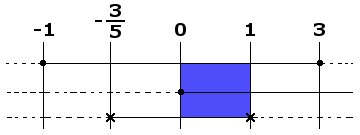

Risolviamo il sistema (b):

$\begin{cases} -x^2+2x+3\ge 0\\ 2x < 0\end{cases}\quad\Rightarrow\quad\begin{cases} -1\le x\le 3\\ x < 0\end{cases}$

Il sistema precedente ha come soluzione $-1\le x < 0$

Uniamo le soluzioni dei sistemi (a) e (b) per trovare la soluzione della disequazione irrazionale 2):

$0\le x < 1\ \vee\ -1\le x < 0\quad\Rightarrow\quad -1\le x < 1$

Infine, mettiamo a prodotto dei segni le soluzioni delle disequazioni 1) e 2):

$$-1\le x < 0\ \vee\ 2 < x \le 3\quad\quad\mbox{a prodotto dei segni con}\quad\quad -1\le x < 1$$

Come si vede dal grafico, la soluzione è quella in corrispondenza dei segni meno, visto che la disequazione di partenza ha verso $<$. Dunque la soluzione è:

$$0 < x < 1\quad\vee\quad 2 < x \le 3$$