Si calcoli l'intervallo di convergenza, precisando il comportamento agli estremi, della seguente serie $$\sum\limits_{n=1}^{+\infty} \frac{(n-1)^2 \cos e^{-(n-1)}}{(1+x^2)^n}$$
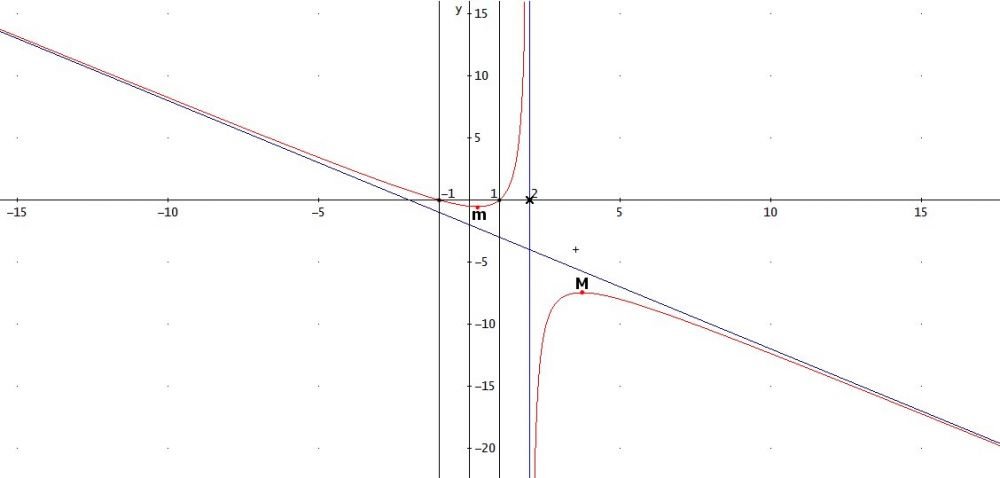
La serie data ha una forma abbastanza complessa, allora cerchiamo una serie che si comporti asintoticamente come quella del testo. Per fare questo basta osservare che $\ \cos \frac{1}{e^{n-1}} \stackrel{\tiny {n \longrightarrow +\infty}}{\longmapsto} 1 \ $ e che quindi il termine generale della serie è asintotico a
$$ \frac{(n-1)^2 \cos e^{-(n-1)}}{(1+x^2)^n} \sim \frac{n^2}{x^{2n}} $$ quando $|x^2|>1$
e che
$$ \frac{n^2}{x^{2n}} \stackrel{\tiny{n \longrightarrow +\infty}}{\longmapsto} 0 $$
Ricordando che la convergenza assoluta implica quella puntuale, studiamo il comportamento della serie dei moduli. Cerchiamo di maggiorare il modulo del termine generale con il termine generale di una serie convergente.
$$|f_n (x)| \leq \frac{(n-1)^2}{(1+x^2)^n} \leq \frac{(n-1)^2}{x^{2n}} $$
L'ultimo termine converge quando $|\frac{1}{x^2}| < 1, \ $ ovvero per
$$ x < -1 \quad \vee \quad x > 1 $$
La serie quindi converge assolutamente in $]-\infty, -1[ \ \cup \ ]1, +\infty[ \quad \Rightarrow $ la serie converge puntualmente in $]-\infty, -1[ \ \cup \ ]1, +\infty[$.
Studiamo il comportamento della serie agli estremi: per $x = \pm 1$ il termine generale della serie diventa
$$f_n(x) = \frac{(n-1)^2 \cos e^{-(n-1)}}{2^n}$$
Per lo stesso motivo di cui sopra, studio la convergenza assoluta:
$$|f_n(x) = \frac{(n-1)^2 \cos e^{-(n-1)}}{2^n}| \leq \frac{(n-1)^2}{2^n} \sim \frac{1}{2^n}$$
che converge. L'intervallo di convergenza è allora $$I_c = ]-\infty, -1] \cup [1, +\infty[ $$
Per concludere l'esercizio, rimane da studiare la convergenza uniforme della serie. Bisogna allora richiedere che in $I_c$ il seguente $sup$ infinitesimo per $n \rightarrow +\infty$
$$\sup_{x \in I_c} \ |f_n(x) - f(x)| \rightarrow 0 \quad \mbox{per }n \rightarrow +\infty $$
Poichè nel nostro caso la funzione limite $f(x)$ nell'intervallo di convergenza è 0, come visto all'inizio dell'esercizio, abbiamo:
$$\sup_{x \in I_c} \ |f_n(x) - f(x)| = \sup_{x\in I_c} |f_n(x)| \leq \sup_{x \in I_c} \frac{(n-1)^2}{(1+x^2)^n} = \sup_{x \in I_c} g_n(x)$$
Studio allora la funzione $g_n(x)$ calcolandone la derivata prima:
$$g'_n (x) = -(n-1)^2 \frac{2nx (1+x^2)^{n-1}}{(1+x^2)^{2n}} = -(n-1)^2 \frac{2nx}{(1+x^2)^{n+1}} > 0 \Leftrightarrow $$ $$-2nx >0 \Leftrightarrow x<0$$
Ricordando che stiamo lavorando in $I_c$, il sup si ha per $x=-1$ quindi
$$\sup_{x \in I_c} \ |f_n(x) - f(x)| \leq \sup_{x \in I_c} g_n(x) = \frac{(n-1)^2}{2^n} \rightarrow 0 \quad \mbox{per }n \rightarrow +\infty $$
quindi la serie converge uniformemente in $I_c$ e l'esercizio è così concluso.
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
