Si consideri un triangolo isoscele ABC. Si tracci l'altezza CH e il punto medio M del segmento AH. Si disegni il punto di intersezione D tra la retta perpendicolare ad AB passante per M e il prolungamento del lato BC. Dimostrare che il quadrilatero ADCH è equivalente al triangolo ABC. (Sug: dimostrare che l'area del quadrilatero e quella del triangolo sono il doppio di quella di un opportuno triangolo)
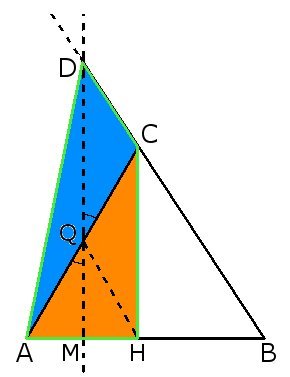
Poichè il triangolo è isoscele, si ha:
$$A_{ABC}=2\cdot A_{ACH}$$
Usando il suggerimento dato, si deduce che bisogna dimostrare che:
$$A_{ADCH}=2\cdot A_{ACH}$$
Osserviamo che il triangolo DQC è equivalente al triangolo CQH perchè triangoli ottenuti dividendo tramite diagonale il parallelogramma DQHC. Inoltre, CQH è equivalente al triangolo AQH (si vede facilmente se divido in due il triangolo CQH). Infine, il triangolo DQC è equivalente al triangolo DQA in quanto il segmento DQ è la mediana del triangolo ADC.
Poichè il quadrilatero ADCH è stato scomposto in 4 triangoli uguali (DQC, CQH, AQH e DQC), risulta essere il doppio del triangolo ABH. Come volevasi dimostrare.
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
