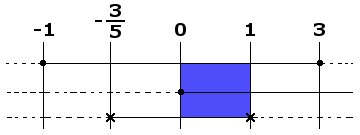
Sia $f:[-2,3[\cup]5,7]\rightarrow\mathbb R$ la funzione definita a tratti avente il seguente grafico:
Quale delle seguenti affermazioni è FALSA?
La risposta esatta è la 5) poichè $\int_0^{5/2}f(x)\ dx$ non è altro che l'area del triangolo che ha vertici in $(0,0),\ (2,-2),\ \left(0,\frac{5}{2}\right)$. Tale area, infatti si calcola nel seguente modo:
$$\int_0^{5/2}f(x)\ dx=-\frac{b\cdot h}{2}=-\frac{\frac{5}{2}\cdot 2}{2}=-\frac{5}{2}\neq-\frac{3}{2}$$
E' altresì facile verificare che le altre asserzioni sono vere: $f$ ha esattamente un punto angoloso (per $x=2$); $f$ ha chiaramente due minimi relativi (per $x=2$ e per $x=6$); il limite si calcola banalmente osservando che il punto di ascissa $1$ ha ordinata pari a $-1$; infine, la funzione calcolata in $\frac{5}{2}$ vale $0$ (ovvero $f(\frac{5}{2})=0$).
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
