Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare...
Si studi la sviluppabilità in serie di Mc-Laurin della seguente funzione $$f(x) = \arctan (\frac{4}{\pi} \arctan x) $$
Esercizio 1
Sappiamo che la funzione $g(x) = \arctan x$ è sviluppabile in serie di Mc-Laurin per ogni $x \in [-1, \ 1]$. Dunque $f(x)$ sarà sviluppabile se
$$ -1 \leq \frac{4}{\pi} \arctan x \leq 1 \quad \Longleftrightarrow \quad -\frac{\pi}{4} \leq \arctan x \leq \frac{\pi}{4} \quad \Longleftrightarrow \quad -1 \leq x \leq 1 $$
L'esercizio non è chiaro?
Altri esercizi di matematica
Problemi di geometria analitica risolti
Problemi di geometria analitica sulle rette
studentiScuola superiore
livello difficoltà
Esercizi sulle equazioni
Problemi geometrici sulle equazioni di secondo grado
studentiScuola superiore
livello difficoltà

Esercizi sulle disequazioni
Disequazioni intere di primo grado
studentiScuola superiore
livello difficoltà

Esercizi svolti sulle trasformazioni geometriche
Verificare se le equazioni rappresentano una trasformazione geometrica
studentiScuola superiore
livello difficoltà

Esercizi di algebra e aritmetica
Disequazioni immediate senza delta
studentiScuola superiore
livello difficoltà
Esercizi di geometria piana
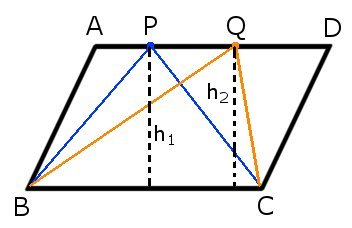
Equivalenza triangoli che si formano da un parallelogramma
studentiScuola superiore
livello difficoltà
Problemi di geometria analitica risolti
Calcolo perimetro e mediane di un triangolo nel piano
studentiScuola superiore
livello difficoltà

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare