Qui di seguito un'anteprima del PDF che contiene esercizi svolti sul calcolo di media, mediana, quartili, percentili, varianza, deviazione standard, campo di variazione, coefficiente di variazione ed errore standard.

Gli esercizi sono stati accuratamente selezionati e raggruppano tutte le possibili tipologie di problemi e quesiti inerenti a:
- indici di centralità quali media e mediana;
- indici di posizione (di NON centralità) quali moda, quartili e percentili;
- indici di variabilità o dispersione come la deviazione standard o scarto quadratico medio, scostamento medio semplice assoluto, varianza, campo di variazione e coefficiente di variazione;
Infatti, ti mostro come calcolare ogni indice di posizione e variabilità nei seguenti casi:
- Dati semplici (distribuzione di valori singoli)
- Distribuzione di frequenza
- Dati raggruppati in classi
In aggiunta, ti fornisco delle formule semplificate per calcolare velocemente i suddetti indici, molto utili se devi svolgere un esame scritto con calcolatrice.
Inoltre, ti svelo alcune proprietà della media aritmetica e della varianza che ti consentono di risolvere alcuni esercizi in cui è necessario un approccio più matematico.
Alla fine trovi anche un esercizio che ti aiuta a capire come leggere i valori dei quartili in un boxplot.
Di seguito ti elenco le tracce degli esercizi svolti che trovi nel PDF:
Siano dati i voti in trentesimi che 10 studenti hanno conseguito in un esame universitario
26, 18, 15, 20, 23, 17, 22, 10, 28, 12
Calcolare:
- voto medio
- moda
- scarto quadratico medio (o deviazione standard) e varianza
- scostamento medio semplice assoluto
e interpretare i risultati.
Supponiamo che i punteggi ottenuti da 10 concorrenti in una gara siano stati i seguenti:
28, 12, 34, 28, 14, 45, 32, 34, 28, 14
Calcola la moda e descrivi il suo significato.
Le 421 famiglie di un piccolo comune italiano sono state classificate secondo il numero X di ordini di acquisto on-line effettuati nell'ultimo Black-Friday, i dati raccolti sono riportati nella tabella seguente

Relativamente al numero di ordini X, calcola:
- il valore medio
- moda
- varianza e deviazione standard
- scostamento medio semplice assoluto
La seguente tabella riporta la distribuzione di 100 imprese artigianali lombarde secondo il numero X di dipendenti al 30.06.2022

Relativamente al numero di dipendenti X, calcola:
- il valore medio
- classe modale
- varianza e deviazione standard
- scostamento medio semplice assoluto
Si riportano di seguito i valori della quantità di ferro (in mg) contenuto in 10 campioni di terreno:
38 27 22 18 20 16 24 26 25 24
Determinare:
- il campo di variazione (o range);
- il coefficiente di variazione.
- Tramite opportuno indice, confrontare la variabilità della suddetta distribuzione con quella di un altro campione di valori di ferro espressi in grammi supposto che quest'ultimo abbia media e deviazione standard rispettivamente pari a 30g e 10,2g. Motivare la scelta dell'indice di variabilità utilizzato.
Un ente di ricerca ha 550 dipendenti di cui 50 sono dirigenti, 100 hanno la qualifica di primo ricercatore e 400 ricercatori. L'età media dei dirigenti è 59 anni, quella dei primi ricercatori è 39 e quella dei ricercatori è 42 anni. Qual è l'età media dei dipendenti in complesso?
La tabella seguente riporta i valori dell'altezza dei 9 alberi di una determinata specie presenti in un'area forestale:

- Calcolare la media
- In seguito alla misurazione ci si è accorti di un errore nella taratura dello strumento di misurazione che ha determinato per ogni albero un'altezza più bassa di 10cm. Determinare il valore corretto dell'altezza media degli alberi.
- Supponi che l'altezza media di un altro campione di 20 alberi sia 131cm. Come varierebbe tale media se si aggiunge un altro albero di altezza 125cm?
Come varia l'errore standard della media campionaria se la dimensione di un campione viene diminuita da 280 a 70?
La tabella seguente riporta la distribuzione della retribuzione annua (in migliaia di Euro) dei 13 dipendenti di una determinata azienda agricola:

- Determinare la varianza della distribuzione
- Ipotizzare che I dirigenti dell'azienda decidano di incrementare la retribuzione annua di tutti i dipendenti del 5%. Come varierebbero la media e la varianza della distribuzione?
- Se invece i dirigenti decidessero di incrementare tutte le retribuzioni di 1.5 migliaia di Euro: come varierebbe la varianza della distribuzione?
Consideriamo i seguenti valori relativi a un'indagine sul numero di bottiglie d'acqua bevute giornalmente da un campione di 5 famiglie:
41, 57, 54, 36, 10
Calcola:
- primo, secondo e terzo quartile;
- 80-esimo percentile o centile;
- quarto decile;
- ricalcola i punti a), b), c) e d) nel caso in cui si aggiungesse all'indagine una 6° famiglia che consuma 13 bottiglie d'acqua al giorno.
Con riferimento all'esercizio 3

Calcola:
- primo, secondo e terzo quartile;
- 99-esimo percentile o centile;
- nono decile.
La tabella rappresenta la distribuzione del fatturato mensile (in migliaia di Euro) di 100 aziende vitivinicole situate in una determinata provincia della regione Toscana
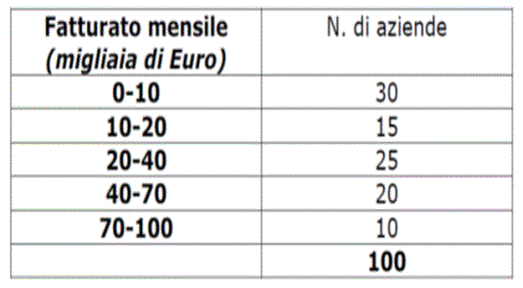
Calcola:
- primo, secondo e terzo quartile;
- 40-esimo percentile o centile;
- settimo decile.
Nel seguente boxplot identificare il valore del ventesimo percentile





