Capita spesso di avere a che fare con una distribuzione di frequenza doppia, ossia una tabella in cui sono presenti le frequenze di due caratteri statistici (vedi approfondimento sulle tabelle di contingenza o a doppia entrata).
Di seguito vediamo come calcolare tramite un esempio la media condizionata a un gruppo di dati di una distribuzione doppia di dati.
Esempio
Il responsabile di un centro medico di un ente pubblico è interessato a studiare le abitudini dei dipendenti rispetto al fumo e all'alcool. Dalla somministrazione di un questionario ai suoi dipendenti ottiene le seguenti informazioni: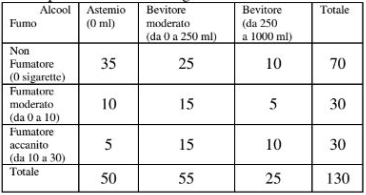
Calcolare la media del numero di sigarette fumate dagli astemi e dai bevitori.
Indichiamo con S la variabile "numero di sigarette fumate" e con A e B rispettivamente i gruppi di persone astemie e bevitori come mostrato nella figura qui in basso.
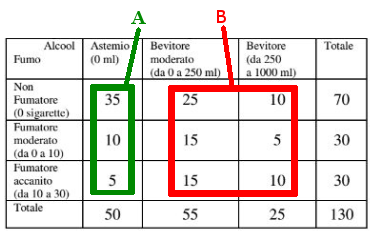
La media del numero di sigarette fumate dagli astemi è la media condizionata $$\begin{array}{l}M(S|A)=\frac{0\cdot 35 + 5\cdot 10+ 20\cdot 5}{50}\\=3\end{array}$$
Mentre invece, la media del numero di sigarette fumate dai bevitori è la media condizionata $$\begin{array}{l}M(S|B)=\frac{0\cdot (25+10) + 5\cdot (15+5)+ 20\cdot (15+10)}{55+25}\\=7.5\end{array}$$
Notiamo che, essendo i dati raggruppati in classi, la media è stata calcolata prendendo i valori centrali della classe cosi come spiegato sopra.
Proprietà associativa della media aritmetica
Supponiamo che X sia il carattere quantitativo di cui vogliamo calcolare la media totale, n siano tutte le osservazioni e $A_1,\dots ,A_k$ siano tutti i gruppi corrispondenti ai caratteri condizionanti di X aventi rispettivamente $n_1,\dots , n_k$ unità statistiche. Allora, la media totale può essere calcolata mediante la proprietà associativa della media aritmetica: $$\bbox[#ffffff,5px,border:2px solid #ff6600]{M(X)=\frac{M(S|A_1)\cdot n_1+\dots +M(S|A_k)\cdot n_k}{n}}$$
In sostanza, la media aritmetica totale di una distribuzione doppia di dati può essere calcolata facendo la media ponderata di tutte le medie condizionate.
Riferendoci alla distribuzione di frequenze dell'esempio precedente, la media totale del numero di sigarette fumate è dato da: $$\begin{array}{l}M(S)=\frac{0\cdot (35+25+10) + 5\cdot (10+15+5)+ 20\cdot (5+15+10)}{130}\\=5.77\end{array}$$
Possiamo adesso verificare che vale la proprietà associativa, infatti: $$\begin{array}{l}M(S)=\frac{M(S|A)\cdot n_A+M(S|B)\cdot n_B}{n}\\=\frac{3\cdot 50+7.5\cdot 80}{130}\\=5.77\end{array}$$



