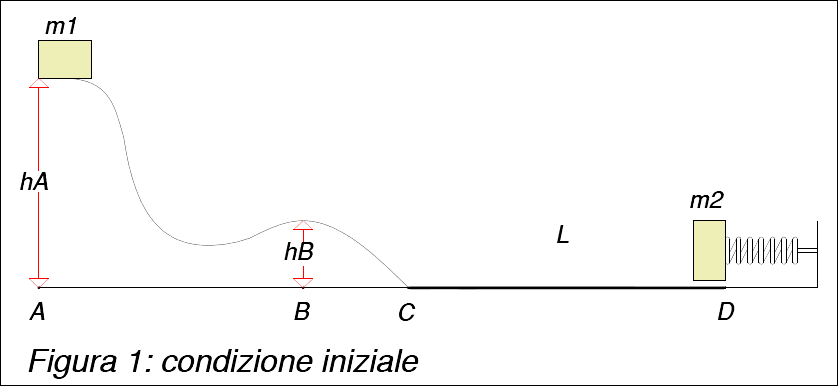
Si consideri un disco omogeneo di raggio $R=20cm$ e massa $M=10kg$ e supponiamo che vi siano saldati due punti materiali $m=M/3$ ad una distanza $r=R/2$ dal centro, in direzione opposta, come mostrato nella figura in basso. Il disco è appoggiato su un piano scabro e ha inizialmente velocità $v_0=3m/s$. Dopo aver percorso uno scalino $h=40cm$, colpisce una molla di costante elastica $k=70N/m$. Si calcoli il valore della compressione massima della molla, assumendo il moto di rotolamento puro durante tutto il percorso.

Dato che un moto di puro rotolamento implica che il lavoro delle forze di attrito sia nullo, possiamo applicare il principio di conservazione dell'energia considerando la sommità del piano come punto iniziale e la posizione della molla come punto finale.
Calcoliamo energia cinetica e potenziale per ogni punto considerato.
L'energia cinetica iniziale è data dalla somma dell'energia cinetica traslazionale e di quella rotazionale: $$E_c^i=\frac{1}{2}(M+2m)v_0^2+\frac{1}{2}I\omega_0^2\quad (1)$$ dove il momento di inerzia $I$ totale è la somma del momento di inerzia del disco rispetto al centro di massa e i momenti di inerzia delle due massi puntiformi $m$: $$I=I_{disco}+2I_m=\frac{1}{2}MR^2+\cancel{2}m\cdot\frac{R^2}{\cancel{4}}=\frac{1}{2}(M+m)R^2$$
Riscriviamo la (1) tenendo conto dell'espressione di $I$ appena ricavata e del fatto che $\omega_0=\frac{v_0}{R}$: $$\begin{eqnarray*} E_c^i &=& \frac{1}{2}(M+2m)v_0^2+\frac{1}{2}\cdot\frac{1}{2}(M+m)\cancel{R^2}\cdot \frac{v_0^2}{\cancel{R^2}} =\\ &=& \frac{1}{2}(M+2m)v_0^2+\frac{1}{4}(M+m)v_0^2=\\ &=& \left(\frac{3}{4}M+\frac{5}{4}m\right)v_0^2 \end{eqnarray*}$$
L'energia potenziale iniziale è: $$E_p^i=(M+2m)\cdot g\cdot h$$
Nel punto in cui il disco raggiunge la base del piano e quindi la molla, avremo soltanto l'energia potenziale da essa generata comprimendosi di un tratto $\Delta x$: $$E_p^f=\frac{1}{2}k(\Delta x)^2$$
Dunque, applicando l'equazione del bilancio energetico si ha: $$\begin{array}{l} E_c^i+E_p^i=E_p^f\\ \left(\frac{3}{4}M+\frac{5}{4}m\right)v_0^2+(M+2m)\cdot g\cdot h=\frac{1}{2}k(\Delta x)^2 \end{array}$$ da cui ci ricaviamo la compressione massima $\Delta x$ della molla $$\begin{eqnarray*} \Delta x &=& \sqrt{\frac{\left(\frac{3}{4}M+\frac{5}{4}m\right)v_0^2+(M+2m)\cdot g\cdot h}{k}}=\\ &=& \sqrt{\frac{\left(15+\frac{5}{2}\cdot\frac{10}{3}\right)\cdot 9+\left(20+\frac{40}{3}\right)\cdot 9.81\cdot 0.4}{70}}=\\ &=& 2.21m \end{eqnarray*}$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare