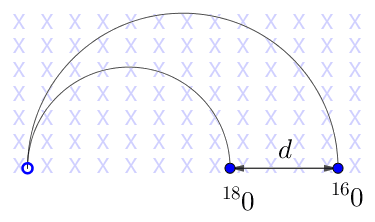
Una nave pirata è ormeggiata a $500$ metri dalla base di un forte che difende l'entrata del porto di un'isola. Il cannone che la protegge, piazzato a livello del mare, ha una velocità di lancio di $82m/s$ (vedi figura). Calcolare:
- a quale alzo (angolo di elevazione $\theta$) si deve puntare il cannone per colpire la nave pirata;
- il tempo di volo in corripondenza dell'alzo maggiore;
- a quale distanza dal porto deve portarsi la nave per essere fuori dalla portata di tiro del cannone.

Il moto del proiettile è un moto uniformemente accelerato lungo la direzione $y$ (perchè sogggetto all'accelerazione di gravità) e un moto rettilineo uniforme lungo la direzione $x$ (poichè la velocità orizzontale è costante). Le equazioni che descrivono il suo spostamento sono quindi: $$\begin{cases} x(t)&=&x_0+v_{0x}t\\ y(t)&=&y_0+v_{0y}t+\frac{1}{2}a_yt^2\end{cases}$$ dove
- $x_0=0$ e $y_0=0$ (posizione iniziale del proiettile);
- $v_{0x}=v_0\cdot\cos\theta$ e $v_{0y}=v_0\cdot\sin\theta$ (componenti della velocità lungo le due direzioni ricavate applicando i teoremi sul triangolo rettangolo);
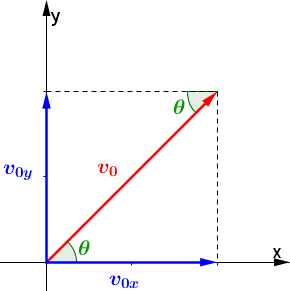
- $a_y=-g$ (accelerazione verticale dovuta alla gravità);
Semplificando e sostituendo nelle due equazioni tali espressioni otteniamo: $$\begin{cases} x(t)&=&v_0\cdot\cos\theta\cdot t\\ y(t)&=&v_0\cdot\sin\theta\cdot t-\frac{1}{2}gt^2\end{cases}$$
Ricaviamoci l'angolo $\theta$ imponendo che l'ascissa del proiettile sia $x(t^*)=d$ e che l'ordinata sia $y(t^*)=0$ ad un certo istante $t^*$ dell'impatto con la nave: $$\begin{cases} d&=&v_0\cdot\cos\theta\cdot t^*\\ 0&=&v_0\cdot\sin\theta\cdot t^*-\frac{1}{2}gt^{*2}\end{cases}$$
Esplicitiamo $t^*$ nella prima equazione e sostituiamolo nella seconda: $$\begin{cases} t^*&=&\frac{d}{v_0\cos\theta}\\ 0&=&v_0\cdot\sin\theta\cdot \frac{d}{v_0\cos\theta}-\frac{1}{2}g\frac{d^2}{v_0^2\cos^2\theta}\end{cases}$$
Risolviamo la seconda equazione appena ottenuta ricavando $\theta$: $$\begin{array}{l} -\frac{1}{2}g\frac{d^2}{v_0^2\cos^2\theta}+\cancel{v_0}\cdot\sin\theta\cdot \frac{d}{\cancel{v_0}\cos\theta}=0\\ -gd^2+\sin\theta\frac{d}{\cancel{\cos\theta}}\cdot 2v_0^2\cos^{\cancel{2}}\theta=0\\ -gd^2+dv_0^2\cdot 2\sin\theta\cos\theta=0\\ -gd^2+dv_0^2\cdot\sin2\theta=0\\ \sin2\theta=\frac{gd^{\cancel{2}}}{\cancel{d}v_0^2}=\frac{gd}{v_0^2}=\frac{9.81\cdot500}{82^2}=0.73\end{array}$$
Le possibili soluzioni della precedente equazione sono date da: $$\begin{array}{l} 2\theta=\arcsin(0.73)\\ 180°-2\theta=\arcsin(0.73)\end{array}$$ ossia $\theta_1=23.44°$ e $\theta_2=66.56°$. Questo vuol dire che ci sono due diverse angolazioni con cui il cannone potrà posizionarsi per colpire la nave.
Il tempo $t^*$ di volo in corrispondenza dell'alzo maggiore ($\theta_2$) è già stato trovato ed è: $$t^*=\frac{d}{v_0\cos\theta_2}=\frac{500}{82\cdot\cos66.56°}=15.33s$$
La distanza a cui dei porsi la nave affinchè non venga colpita dal cannone coincide con la gittata massima. Questa può essere calcolata considerando nuovamente il sistema con le due equazioni dello spostamento, imponendo $x(t)=x_G$ e $y=0$: $$\begin{cases} x_G&=&v_0\cdot\cos\theta\cdot t\\ 0&=&v_0\cdot\sin\theta\cdot t-\frac{1}{2}gt^2\end{cases}$$
Sostituendo il tempo $t$ ricavato dalla prima equazione ($t=x_G/(v_0\cos\theta)$) nella seconda, dopo alcuni passaggi otteniamo: $$\begin{array}{l} -gx_G^2+x_Gv_0^2\cdot\sin2\theta=0\\ gx_G^2-x_Gv_0^2\cdot\sin2\theta=0\\ x_G(gx_G-v_0^2\cdot\sin2\theta)=0\end{array}$$ da cui, trascurando la soluzione non significativa $x_G=0$, otteniamo $gx_G-v_0^2\cdot\sin2\theta=0$, ossia: $$x_G=\frac{v_0^2-\sin2\theta}{g}$$ che è l'espressione della gittata del proiettile.
Ricaviamoci la gittata massima derivando rispetto a $\theta$ tale espressione: $$x_G'=\frac{2v_0^2\cos2\theta}{g}$$
Risolvendo $x_G'=0$ otteniamo l'angolo $\theta$ che massimizza la gittata: $$\frac{2v_0^2\cos2\theta}{g}=0\quad\Rightarrow\quad cos2\theta=0 \quad\Rightarrow\quad \theta=45°$$
Dunque la distanza cercata si trova sostituendo nell'espressione di $x_G$ il valore di $\theta$ appena trovato: $$x_G=\frac{82^2-\sin90°}{9.81}=685.42m$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare