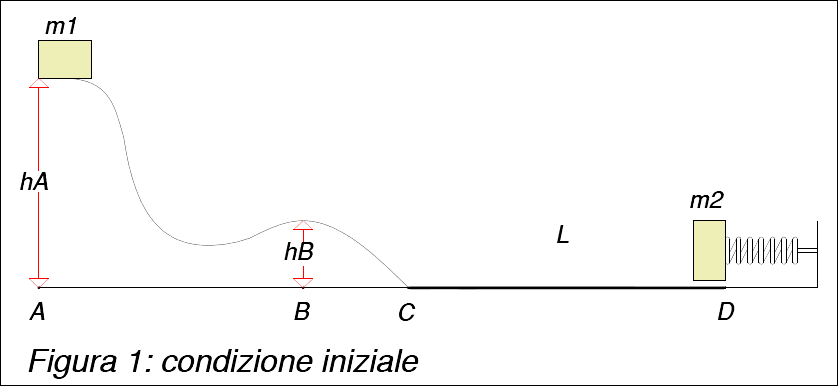
Un corpo di massa $m_1=400g$ viene lanciato da un'altezza $h_A=30cm$ e con velocità $v_A=0.5m/s$ giù per uno scivolo privo di attrito. Giunto alla fine dello scivolo (punto C) il corpo percorre un tratto orizzontale CD lungo $L=30cm$ e con coefficiente di attrito $\mu=0.2$. Dopo di che il corpo urta anelasticamente contro una massa $m_2=100g$ collegata ad una molla di costante elastica $k=70N/m$. Si consideri inoltre che l'altezza nel punto B è di $h_B=10cm$ rispetto alla base. Calcolare:
- l'energia cinetica del corpo in B;
- la lunghezza $\Delta x$ di compressione della molla in seguito all'urto del corpo;
- il lavoro delle forze non conservative;
- l'energia meccanica totale nei punti A, B, C, D e nell'istante in cui la molla è compressa.
PUNTO a)
L'assenza di attrito e quindi di forze non conservative, ci permette di poter applicare il teorema sulla conservazione dell'energia nel tratto AB: $$E_{cin}^A+E_{pot}^A=E_{cin}^B+E_{pot}^B$$ e quindi di poter calcolare l'energia cinetica nel punto B: $$\begin{eqnarray} E_{cin}^B &=&E_{pot}^A+E_{cin}^A-E_{pot}^B=m_1gh_A+\frac{1}{2}m_1v_A^2-m_1gh_B\\ &=& 0.4\cdot 9.81\cdot 0.3+\frac{1}{2}\cdot 0.4\cdot 0.5^2-0.4\cdot 9.81\cdot 0.1=0.83J\end{eqnarray}$$
Calcoliamo anche la velocità $v_B$ perchè ci servirà successivamente: $$E_{cin}^B=\frac{1}{2}m_1v_B^2\quad\Rightarrow\quad v_B=\sqrt{\frac{2E_{cin}^B}{m_1}}=\sqrt{\frac{2\cdot 0.83}{0.4}}=2.04m/s$$
PUNTO b)
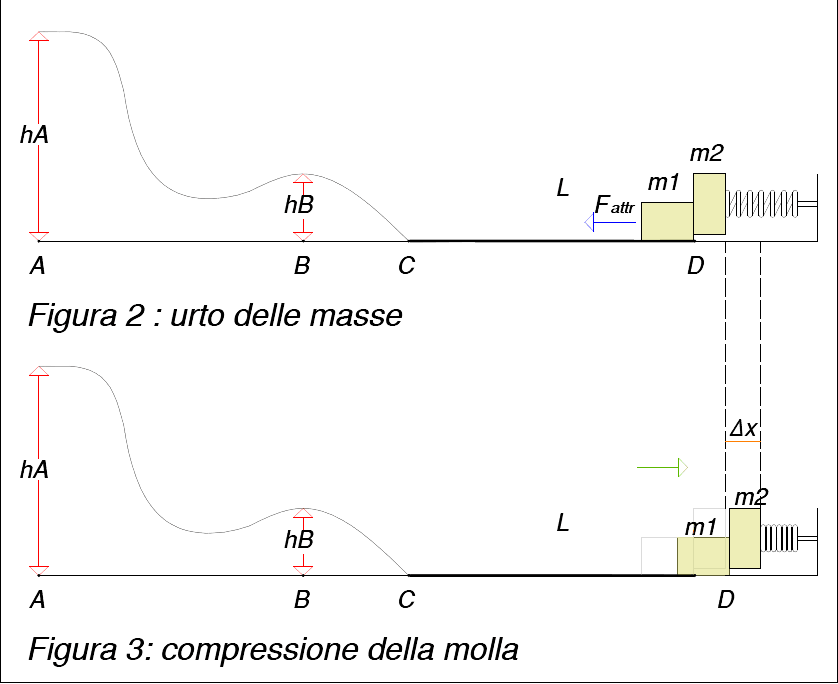
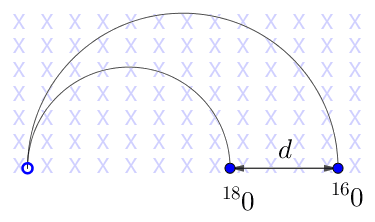
Supposto nullo l'attrito nel tratto $\Delta x$ percorso dalle due masse in seguito all'urto, possiamo applicare la conservazione dell'energia cinetica in tale tratto eguagliando l'energia cinetica finale della molla con l'energia cinetica iniziale dovuta alla massa $m_1$ che urta in D l'altra massa con velocità $v_D$: $$\cancel{\frac{1}{2}}k\Delta x^2=\cancel{\frac{1}{2}}m_1v_D^2$$ da cui otteniamo: $$\Delta x=\sqrt{\frac{m_1v_D^2}{k}}$$
Per ricavare $v_D$ basta applicare la conservazione dell'energia nel tratto liscio BC $$\begin{array}{l} E_{cin}^B+E_{pot}^B=E_{cin}^C+E_{pot}^C\\ \frac{1}{2}\cancel{m}v_B^2+\cancel{m}gh_B=\frac{1}{2}\cancel{m}v_C^2\end{array}$$ da cui otteniamo $v_C$ $$v_C=\sqrt{v_B^2+2gh_B}=\sqrt{2.04^2+2\cdot 0.1}=2.09m/s$$
Dopodichè, per il teorema lavoro-energia applicato nel tratto scabro CD si ha: $$\begin{eqnarray} L_{attrito}&=&E_{cin}^D-E_{cin}^C\\ -F_a\cdot L&=&\frac{1}{2}m_1v_D^2-\frac{1}{2}m_1v_C^2\\ -\mu\cancel{m_1}g\cos\theta\cdot L&=&\frac{1}{2}\cancel{m_1}v_D^2-\frac{1}{2}\cancel{m_1}v_C^2\end{eqnarray}$$ da cui $$v_D=\sqrt{-2\mu g\cos\theta\cdot L+v_C^2}=\sqrt{-2\cdot 0.2\cdot 9.81\cos\frac{\pi}{2}\cdot 0.3+2.09^2}=1.79m/s$$
Una volta trovato $v_D$ possiamo trovare la lunghezza $\Delta x$ con la formula ricavata inizialmente: $$\Delta x=\sqrt{\frac{m_1v_D^2}{k}}=\sqrt{\frac{0.4\cdot 1.79^2}{70}}=0.14$$
PUNTO c)
L'unica forza non conservativa e la forza di attrito e il lavoro prodotto è: $$L_{attrito}=-\mu m_1g\cos\theta\cdot L=-0.2\cdot 0.4\cdot 9.81\cos\frac{\pi}{2}\cdot 0.3=-0.24J$$
PUNTO d)
Determiniamo le energie meccaniche totali nei vari punti: $$\begin{eqnarray} E_{mecc}^A&=&E_{cin}^A+E_{pot}^A=\frac{1}{2}m_1v_A^2+m_1gh_A=\frac{1}{2}\cdot 0.4\cdot 0.5^2+0.4\cdot 9.81\cdot 0.3=1.23J\\ E_{mecc}^B&=&E_{cin}^B+E_{pot}^B=\frac{1}{2}m_1v_B^2+m_1gh_B=\frac{1}{2}\cdot 0.4\cdot 2.04^2+0.4\cdot 9.81\cdot 0.1=1.22J\\ E_{mecc}^C&=&E_{cin}^C=\frac{1}{2}m_1v_C^2=\frac{1}{2}\cdot 0.4\cdot 2.09^2=0.87J\\ E_{mecc}^D&=&E_{cin}^D=\frac{1}{2}m_1v_D^2=\frac{1}{2}\cdot 0.4\cdot 1.79^2=0.64J\\ E_{mecc}^{molla}&=&\frac{1}{2}k\Delta x^2=\frac{1}{2}\cdot 0.3\cdot 0.14^2=0.003J\end{eqnarray}$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare