Una sferetta conduttrice carica molto leggera di massa $m = 2 \cdot 10^{-3} Kg$ possiede una carica $q_2 = 2 \cdot 10^{-8} C$ ed è sospesa ad un filo di lunghezza $l$. Una seconda sferetta conduttrice con una carica $q_1= 5 \cdot 10^{-7} C$ viene avvicinata a $q_2$. Quando la distanza tra i due centri di $q$ e $q_0$ è $5 cm$ l'angolo che il filo forma con la verticale è $\alpha$. Calcolare il valore di tale angolo $\alpha$.
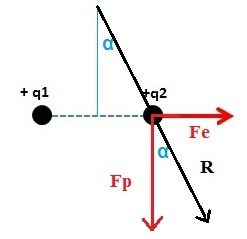
Le forze che agiscono su $q_2$ sono la forza peso e la forza elettrostatica dovuta alla carica di prova $q_1$. La loro forza risultante $R$ sarà bilanciata dalla forza elastica del filo ed essa avrà la stessa direzione del filo.
I vettori "forza peso" e "forza elettrostatica" sono dunque i cateti di un triangolo rettangolo simile a quello che il filo forma con la congiungente dei due centri delle sfere conduttrici e con la verticale. Sapendo, adesso, che in un triangolo rettangolo un cateto è uguale all'altro cateto per la tangente dell'angolo opposto, avremo che:
$$F_e = F_p \cdot tg \alpha$$ da cui $$\alpha= arctg \frac{F_e}{F_p}$$ dove abbiamo indicato con $F_e$ la forza elettrostatica e con $F_p$ la forza peso.
In particolare $$F_e = \frac{1}{4 \pi \epsilon_0}\frac{q_1 q_2}{r^2}$$ dove ricordiamo che $r$ è la distanza tra le due cariche, quindi $r = 5 \cdot 10^{-2} m$. Andando a sostituire i dati del problema si ha $$F_e = \frac{1}{4 \pi \epsilon_0}\frac{q_1 q_2}{r^2} = 9 \cdot 10^{9} \frac{5 \cdot 10^{-7} \cdot 2 \cdot 10^{-8}}{25 \cdot 10^{-4}} = 3.6 \cdot 10^{-2} N $$
Mentre la forza peso risulta $$F_p = m \cdot g = 2 \cdot 10^{-3} \cdot 9.8 = 19.6 \cdot 10^{-3} N$$
Si avrà allora $$\alpha= arctg \frac{3.6 \cdot 10^{-2} N}{19.6 \cdot 10^{-3}} N = 61°$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare