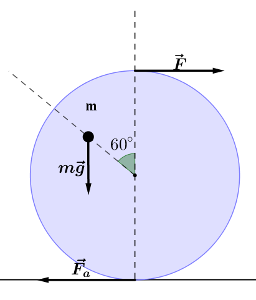
Si consideri un disco omogeneo di raggio $R=20cm$ e massa $M=10kg$. Il disco è appoggiato su un piano scabro. Sul disco è saldato un punto materiale di massa $m=M/3$, ad una distanza $r=R/2$ dal centro del disco e un angolo di $60°$ rispetto alla verticale. Il sistema è mantenuto in equilibrio statico da una forza $F$ applicata in direzione orizzontale sull'estremo superiore del disco, come mostrato in figura. Si calcoli il valore di $F$.
Grafichiamo la forza di attrito che agisce sul disco e la forza peso che agisce sul punto materiale.
Imponiamo la prima condizione di equilibrio (o seconda legge della dinamica) lungo la direzione orizzontale per ricavarci il valore della forza di attrito dovuta al piano e agente sul disco in direzione opposta alla forza $F$: $$\begin{array}{l} \sum F_x =0\\ F-F_a=0\\ F_a=F\ \large\star \end{array}$$
La seconda condizione di equilibrio lungo la direzione verticale è data dalla sommatoria dei momenti delle forze (prodotto vettoriale tra forza e braccio) agenti sul disco. In particolare, considerando che
la seconda equazione cardinale sull'equilibrio dei corpi rigidi è: $$F_a\cdot R + F\cdot R - mg\cdot\frac{R}{2}\sin(120°)=0$$
Semplifichiamo quest'ultima equazione tenendo conto della $\large\star$ e calcoliamo il valore di $F$: $$\begin{array}{l} F\cdot R + F\cdot R - mg\cdot\frac{R}{2}\sin(2\pi /3)=0\\ R\left(2F-\frac{m}{2}g\sin(2\pi /3)\right)=0\\ 2F=\frac{M}{6}g\sin(2\pi /3)\\ F=\frac{M}{12}g\sin(2\pi /3)=7,08N\end{array}$$
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
