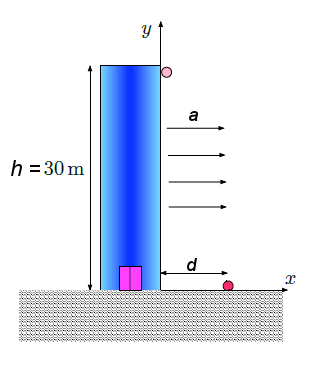
Un oggetto viene lasciato cadere da una torre alta $30m$. Durante la caduta, a causa di un forte vento, subisce una accelerazione costante orizzontale, direzione dell’asse $x$, di modulo $a=15 m/s^2$. Determinare
- la traiettoria descritta dall’oggetto;
- il tempo impiegato per toccare il suolo;
- la distanza d dalla base della torre;
- le componenti della velocità e il suo modulo.
PUNTO a)
Il moto dell'oggetto in caduta libera è un moto uniformemente accelerato nelle due direzioni $y$ e $x$ dato che interviene anche l'accelerazione orizzontale. Le equazioni che lo descrivono sono quindi: $$\begin{cases} x(t)&=&x_0+v_{0x}t+\frac{1}{2}a_xt^2\\ y(t)&=&y_0+v_{0y}t+\frac{1}{2}a_yt^2\end{cases}$$ dove
- $x_0=0$ e $y_0=h$ (posizione iniziale dell'oggetto sul piano);
- $v_{0x}=v_{0y}=0$ (componenti iniziali della velocità lungo le due direzioni; sono entrambe nulle perchè l'oggetto parte da fermo);
- $a_x=a$ (accelerazione orizzontale dovuta al vento);
- $a_y=-g$ (accelerazione verticale dovuta alla gravità);
Dunque, le due equazioni semplificate diventano: $$\begin{cases} x(t)&=&\frac{1}{2}at^2\\ y(t)&=&h-\frac{1}{2}gt^2\end{cases}$$
Per ricavarci l'equazione della traiettoria dobbiamo esprimere la $y$ in funzione della $x$, facendo dunque scomparire la variabile $t$. Esplicitiamo dalla prima delle precedenti equazioni $t^2$ e la sostituiamo nella seconda: $$\begin{cases} t^2&=&\frac{2x}{a}\\ y&=&h-\frac{gx}{a}\end{cases}$$
Sostituendo i numeri nell'espressione della $y$ appena trovata, otteniamo l'equazione della traiettoria: $$y=30-\frac{9.81}{15}x$$
PUNTO b)
Il tempo $\overline{t}$ impiegato per toccare il suolo si trova facilmente imponendo $y=0$ nell'equazione dello spostamento lungo la direzione verticale e risolvendo rispetto a $t$, ossia: $$h-\frac{1}{2}gt^2=0\quad\Rightarrow\quad t^2=\frac{2h}{g}\quad\Rightarrow\quad \overline{t}=\sqrt{\frac{2h}{g}}=\sqrt{\frac{60}{9.81}}=2.47s$$
PUNTO c)
L'ascissa $x=d$ in cui l'oggetto si trova quando arriva al suolo si determina invece a partire dall'equazione dello spostamento lungo la direzione orizzontale nell'istante $\overline{t}$ calcolato nel punto precedente: $$d=\frac{1}{2}a\overline{t}^2=\frac{1}{2}\cdot 15\cdot(2.47)^2=45.76m$$
PUNTO d)
Infine, ricondando che la velocità è definita come la derivata dell'espressione della posizione rispetto al tempo, le componenti della velocità sono: $$\begin{cases} v_x(t)&=&\frac{dx(t)}{dt}=\frac{1}{2}a\cdot 2t=at\\ v_y(t)&=&\frac{dy(t)}{dt}=-\frac{1}{2}g\cdot 2t=-gt\end{cases}$$ mentre il modulo del vettore velocità è: $$|v(t)|=\sqrt{v_x^2+v_y^2}=\sqrt{a^2t^2+g^2t^2}=t\sqrt{a^2+g^2}$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare