Sia data la funzione con valore assoluto
$$f(x)=|x-1|+|x+1|\ \forall x\in\mathbb R$$
Quale tra le seguenti asserzioni è FALSA?
Senza effettuare il solito studio di funzioni notiamo che, con alcuni accorgimenti, possiamo sbarazzarci dei due valori assoluti. Infatti:
Se $x\ge 1\quad\Rightarrow\quad f(x)>0\quad\Rightarrow\quad f(x)=x-1+x+1=2x$
Se $-1\le x < 1\quad\Rightarrow\quad x-1 < 0\quad\Rightarrow\quad f(x)=-(x-1)+x+1=-x+1+x+1=2$
Se $x < -1\quad\Rightarrow\quad f(x) < 0\quad\Rightarrow\quad f(x)=-(x-1)-(x+1)=-x+1-x-1=-2x$
In definitiva, abbiamo che:
$$f(x)=\begin{cases} 2x & \mbox{ se } x\ge 1\\ 2 & \mbox{ se } -1\le x < 1\\ -2x & \mbox{ se } x < -1\end{cases}$$
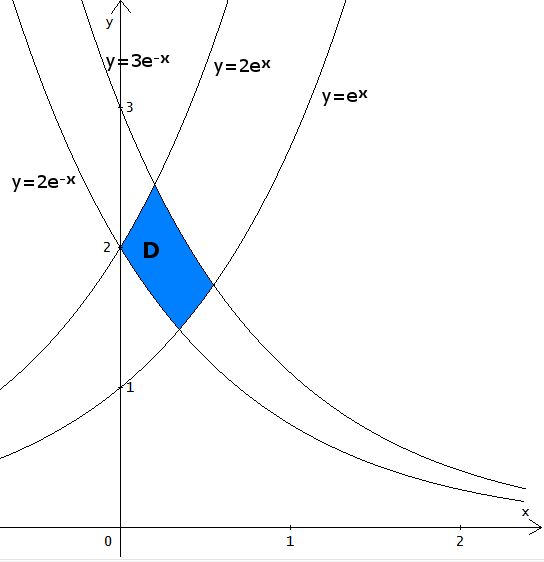
Grazie alla semplicità della funzione appena trovata, possiamo subito disegnare il grafico:
L'affermazione falsa è la 3) in quanto:
$\begin{array}{l} \int\limits_{-2}^2 f(x)\ dx=\int\limits_{-2}^{-1}-2x\ dx+\int\limits_{-1}^12\ dx+\int\limits_1^2 2x\ dx=\\ =\left[-2\frac{x^2}{2}\right]_{-2}^{-1}+\left[2x\right]_{-1}^1+\left[2\frac{x^2}{2}\right]_{1}^{2}=\left[-x^2\right]_{-2}^{-1}+\left[2x\right]_{-1}^1+\left[x^2\right]_{1}^2=\\ =-1+4+2+2+4-1=10\end{array}$
Guardando il grafico, si verifica facilmente che le altre asserzioni sono vere.
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare
