Studio funzione razionale fratta

Poichè nella funzione compare una frazione, dobbiamo escludere tutti i valori di $x$ che annullano il denominatore. Quindi il dominio sarà:

$$2-x\neq 0\quad\Rightarrow\quad x\neq 2$$

Positività

Studiamo il segno della funzione ponendola maggiore di $0$, ovvero, risolviamo la seguente disequazione:

$$\frac{x^2-1}{2-x}>0$$

Risolviamo la disequazione fratta ponendo numeratore e denominatore maggiori di $0$ (vedi qui come si risolve una disequazione fratta)

$$x^2-1>0\quad\Rightarrow\quad x < -1\ \vee\ x >1$$ $$2-x>0\quad\Rightarrow\quad x < 2$$

Facciamo il prodotto dei segni tra queste due soluzioni trovate graficandole sulla retta reale:

Dal grafico si vede che la funzione è positiva per $x < -1\ \vee\ 1 < x < 2$.

Limiti

Calcoliamo i limiti per $x$ che tende a $2$ da destra e da sinistra e i limiti a $\pm\infty$:

$$\lim\limits_{x\rightarrow 2^-}\frac{x^2-1}{2-x}=\left[\frac{3}{0^+}\right]=+\infty$$ $$\lim\limits_{x\rightarrow 2^+}\frac{x^2-1}{2-x}=\left[\frac{3}{0^-}\right]=-\infty$$ $$\lim\limits_{x\rightarrow -\infty}\frac{x^2-1}{2-x}=+\infty$$ $$\lim\limits_{x\rightarrow +\infty}\frac{x^2-1}{2-x}=-\infty$$

Essendo i limiti a $\pm\infty$ uguali a $\pm\infty$, possono esistere asintoti obliqui. Verifichiamone l'esistenza:

$$m=\lim\limits_{x\rightarrow +\infty}\frac{\frac{x^2-1}{2-x}}{x}=\lim\limits_{x\rightarrow +\infty}\frac{x^2-1}{2x-x^2}=\frac{1}{-1}=-1$$ $$\begin{array}{l} q&=\lim\limits_{x\rightarrow +\infty}\frac{x^2-1}{2-x}-(-1)x=\lim\limits_{x\rightarrow +\infty}\frac{x^2-1}{2-x}+x=\\ &=\lim\limits_{x\rightarrow +\infty}\frac{x^2-1+2x-x^2}{2-x}=\lim\limits_{x\rightarrow +\infty}\frac{2x-1}{2-x}=\frac{2}{-1}=-2\end{array}$$

In definitiva, abbiamo trovato un asintoto obliquo di equazione

$$y=-x-2$$

Derivata prima

$$f'(x)=\frac{2x(2-x)-(x^2-1)(-1)}{(2-x)^2}=\frac{4x-2x^2+x^2-1}{(2-x)^2}=\frac{-x^2+4x-1}{(2-x)^2}$$

Per determinare la crescenza, la decrescenza e gli eventuali punti di minimo e di massimo relativo, poniamo la derivata prima maggiore di $0$:

$$\begin{array}{l} &\frac{-x^2+4x-1}{(2-x)^2}>0\quad\Rightarrow\quad -x^2+4x-1>0\quad\Rightarrow\\ &\Rightarrow\quad x^2-4x+1 < 0\quad\Rightarrow\quad 2-\sqrt{3} < x < 2+\sqrt{3}\end{array}$$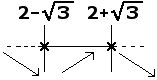 

Le frecce nel grafico indicano dove la funzione è crescente e dove invece è decrescente. Inoltre, in corrispondenza dei punti $x=2-\sqrt{3}$ e $x=2+\sqrt{3}$ abbiamo rispettivamente un punto di minimo relativo e massimo relativo.

Derivata seconda

$$\begin{array}{l} f''(x)&=\frac{(-2x+4)(2-x)^2-(-x^2+4x-1)(-2)(2-x)}{(2-x)^4}=\\ &=\frac{(2-x)[(-2x+4)(2-x)+2(-x^2+4x-1)]}{(2-x)^4}=\\ &=\frac{(2-x)(-4x+2x^2+8-4x-2x^2+8x-2)}{(2-x)^4}=\\ &=\frac{(2-x)6}{(2-x)^4}\end{array}$$

Per vedere dove la funzione è concava, dove è convessa e trovare gli eventuali punti di flesso, poniamo la derivata seconda maggiore di $0$:

$$\frac{(2-x)6}{(2-x)^4}>0\quad\Rightarrow\quad 2-x>0 \quad\Rightarrow\quad x < 2$$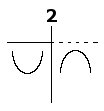

Dallo studio del segno della derivata seconda si vede che la funzione è convessa per $x<2$ mentre è concava per $x>2$. Per $x=2$ non abbiamo un punto di flesso perchè esso è un punto di discontinuità per la funzione!

Concludiamo mostrando il grafico completo della funzione:

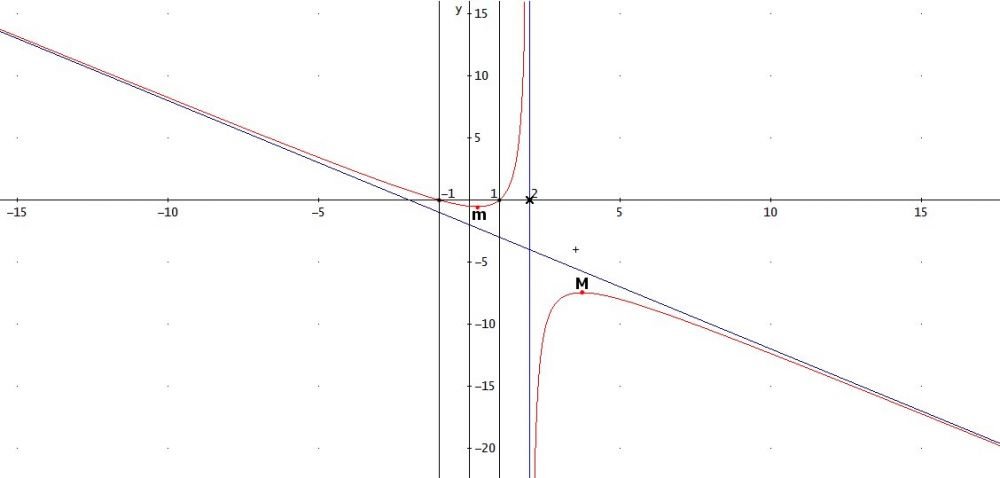
Si vede immediatamente dal grafico che la funzione non ha flessi, quindi la risposta falsa è la 1).

Risulta facile verificare che le altre asserzioni sono vere: banalmente $f$ è illimitata sia superiormente che inferiormente; $f(x)$ è negativa o nulla nell'intervallo $[-1,1]$; $f$ chiaramente non è iniettiva in quanto posso sempre prendere ad esempio $x_1\in]1,2[$ e $x_2\in]-\infty,-1[$ tali che $f(x_1)=f(x_2)$; infine è pure vero che $f$ ristretta a $]-\infty,2[$ è convessa.

Vai agli altri esercizi