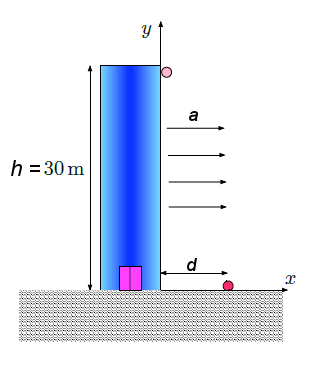
Il cavo di un ascensore di massa $m=2000 Kg$ si spezza quando l'ascensore è fermo al primo piano a distanza $d=4 m$ da una molla di attenuazione di costante elastica $k=1.5\cdot10^5 N/m$. Un dispositivo di sicurezza agisce sulle guide dell'ascensore in modo da far loro sviluppare una forza d'attrito costante $F_a=4900 N$ che si oppone al moto dell'ascensore.
- Calcolare la velocità dell'ascensore prima che urti la molla.
- Trovare di quanto si comprime la molla.
- Calcolare a quale distanza $h$ risale l'ascensore.
- Qual è la distanza complessiva percorsa dall'ascensore prima di fermarsi definitivamente?
PUNTO a)
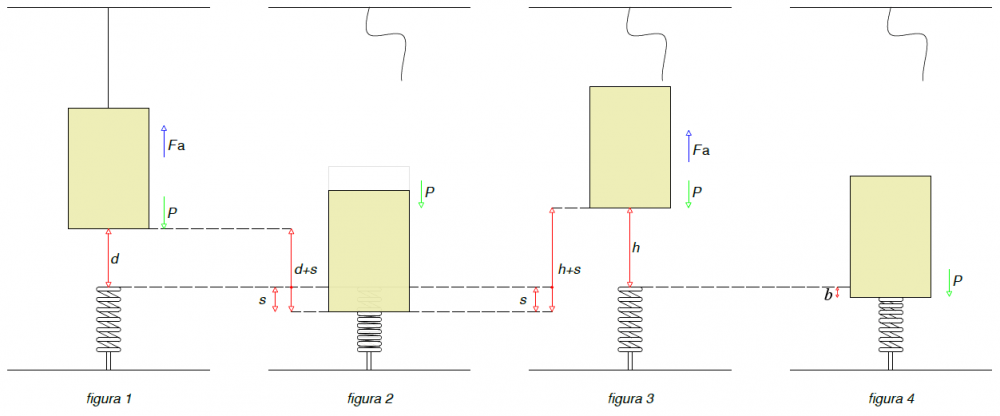
A causa della forza d'attrito provocata dalle guide dell'ascensore, il sistema non è conservativo, ragion per cui non possiamo applicare il teorema sulla conservazione dell'energia meccanica. Ma possiamo sempre applicare il teorema sul lavoro e l'energia ($L_{tot}=\Delta E_{cin}$), in particolare, considerando come istante iniziale, l'istante in cui l'ascensore è ancora sostenuto dal cavo e come istante finale quello in cui l'ascensore urta la molla (figura 1).
Il lavoro totale è dunque dato dalla somma del lavoro svolto dalla forza di attrito e quello svolto dalla forza peso: $$L_{tot}=L_{attrito}+L_{peso}=-F_a\cdot d+F_p\cdot d=(-F_a+mg)\cdot d$$ mentre la variazione di energia cinetica coincide con l'energia cinetica finale dell'ascensore poichè quella iniziale è nulla visto che la sua velocità iniziale è nulla: $$\Delta E_{cin}=E_{cin}^f-E_{cin}^i-=\frac{1}{2}mv_f^2$$
Applicando il teorema sul lavoro e l'energia otteniamo la velocità richiesta $v_f$: $$(-F_a+mg)\cdot d=\frac{1}{2}mv_f^2$$ da cui: $$v_f=\sqrt{\frac{2d(-F_a+mg)}{m}}=\sqrt{\frac{2\cdot 4(-4900+2000\cdot 9.81)}{2000}}=7.67\frac{m}{s}$$
PUNTO b)
Applichiamo nuovamente il teorema sul lavoro e l'energia, ma stavolta dal punto di contatto tra l'ascensore e la molla e il primo arresto (figura 2). Indichiamo con $s$ la compressione della molla. Notiamo che il lavoro della forza di attrito e della forza peso si compiono entrambi sulla distanza $s$; rispetto al caso precendete, dobbiamo aggiungere il lavoro della forza elastica: $$L_{tot}=L_{attrito}+L_{peso}+L_{molla}=-F_a\cdot s+mg s-\frac{1}{2}ks^2$$ e poichè la velocità finale (nell'istante in cui la molla è compressa al massimo dall'ascensore) è nulla si ha: $$\Delta E_{cin}=E_{cin}^f-E_{cin}^i=0-\frac{1}{2}mv_f^2=-\frac{1}{2}mv_f^2$$
Per il teorema sul lavoro e l'energia quindi: $$-F_a\cdot s+mg s-\frac{1}{2}ks^2=-\frac{1}{2}mv_f^2$$ da cui, dopo alcuni passaggi otteniamo la seguente equazione di secondo grado in $s$: $$ks^2-2(-F_a+mg)s-mv_f^2=0$$
Sostituendo a quest'ultima i numeri e risolvendola otteniamo: $$1.5s^2-2(0.15)s-1.2=0\quad\Rightarrow\quad s=\frac{0.15+\sqrt{0.15^2+1.2\cdot 1.5}}{1.5}=1m$$ PUNTO c)
Applichiamo ancora lo stesso teorema, tra l'istante di arresto del'ascensore sulla molla compressa ed il primo arresto in alto dello stesso (figura 3). Indichiamo con $h$ l'altezza raggiunta dall'ascensore in salita. Notiamo che il lavoro della forza di attrito e quello della forza peso si compiono entrambi sulla distanza $s+h$; chiaramente, il lavoro della forza elastica si compierà soltanto sul tratto $s$. L'energia cinetica sarà nulla sia nell'istante iniziale che in quello finale dato che le rispettive velocità sono nulle:
$$-F_a(h+s)-mg(h+s)+\frac{1}{2}ks^2=0$$ da cui, dopo alcuni passaggi si ricava l'altezza $h$: $$h=\frac{\frac{1}{2}ks^2-mgs-F_as}{mg+F_a}= \frac{\frac{1}{2}1.5\cdot 10^5-2000\cdot 9.81-4900}{2000\cdot 9.81+4900}=2.059m$$
PUNTO d)
Quando l'ascensore si ferma, si raggiunge l'equilibrio delle forse agenti su di esso (figura 4); ossia la forza peso risulta essere uguale alla forza elastica. La molla sarà compressa di una quantità che indichiamo con $b$: $$F_p=F_{elastica}\quad\Rightarrow\quad mg=kb$$ da cui possiamo ricavare $b$: $$b=\frac{mg}{k}=\frac{2000\cdot 9.81}{1.5\cdot 10^5}=0.13m$$
Indichiamo poi con $x$ la distanza percorsa a partire dal distacco dell'ascensore dal cavo fino alla fine del moto. Applichiamo anche in questo caso il teorema lavoro-energia: $$+F_ax+\frac{1}{2}kb^2-mg(d+b)=0$$ da cui: $$x=\frac{-\frac{1}{2}kb^2+mg(d+b)}{F_a}=\frac{-\frac{1}{2}1.5\cdot 10^5\cdot 0.13^2+2000\cdot 9.81(4+0.13)}{4900}=1,43m$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare