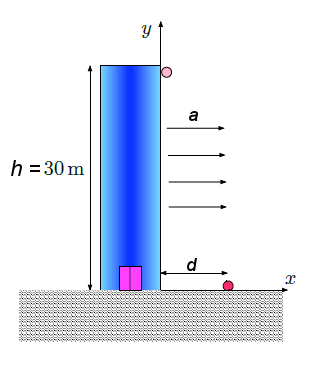
Si consideri il disco di massa $M=10kg$ e raggio $R=20cm$ di questo esercizio. Supponiamo di rimuovere il punto materiale $m$ e di applicare una forza $F=4N$. Se al tempo $t=0$ il disco è fermo, qual è la velocità al tempo $t*=8s?$

Il disco non è più in equilibrio come nell'esercizio precedente, ma inizia a ruotare una volta che la massa puntiforme viene tolta. Il moto di un corpo che ruota è sia traslatorio (lungo l'orizzontale) e sia rotatorio. E' necessario quindi scrivere le due equazioni che regolano tali moti.
In particolare, il moto traslatorio viene descritto dalla seconda della dinamica $\sum F=m\cdot a$: $$F-F_a=M\cdot a_{cm}\quad (1)$$ con $a_{cm}$ l'accelerazione del centro di massa del disco che coincide con l'accelerazione del centro del disco.
Invece, il moto rotatorio è descritto dall'equazione della dinamica rotazionale $\sum \tau =I\cdot \alpha$: $$F_a\cdot R + F\cdot R=I_{cm}\cdot\alpha\quad (2)$$ dove al primo membro compaiono i momenti delle forze agenti sul disco, mentre nel secondo membro abbiamo il prodotto tra il momento di inerzia del centro di massa del disco $I_{cm}=\frac{1}{2}MR^2$ e la sua accelerazione angolare $\alpha$.
Risolviamo il sistema formato dalle due equazioni appena scritte per ricavarci $a_{cm}$. Dalla (1) esplicitiamo $F_a$ $$F_a=F-M\cdot a_{cm}$$ e sostituiamola nella (2) ricordando che l'accelerazione angolare $\alpha=\frac{a_{cm}}{R}$: $$\begin{array}{l} (F-M\cdot a_{cm})R+FR=\frac{1}{2}MR^{\cancel{2}}\cdot\frac{a_{cm}}{\cancel{R}}\\ 2F\cancel{R}-Ma_{cm}\cancel{R}=\frac{1}{2}M\cancel{R}a_{cm}\\ a_{cm}=\frac{4F}{3M}=\frac{16}{30}=0.53\frac{m}{s^2}\end{array}$$
Dato che il moto traslatorio è un moto uniformemente accelerato, la velocità del centro di massa del disco nel generico istante $t$ è data da: $$v_{cm}(t)=a_{cm}t$$
Per $t=8s$ avremo dunque: $$v_{cm}(8)=0.53\cdot 8=4.24\frac{m}{s}$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare