Un fascio di ossigeno sei volte ionizzato viene accelerato da una d.d.p. $V=15MV$. Successivamente esso viene iniettato in un campo magnetico con $|\vec{B}|=1T$, diretto perpendicolarmente alla direzione del fascio. Calcolare la distanza tra gli isotopi $^{16}0$ e $^{18}0$ quando escono dal campo magnetico dopo aver percorso una semicirconferenza. ($m_P= 1,67\cdot 10-27 Kg$)
Il fascio di ossigeno ionizzato 6 volte, acquista 6 protoni, per cui la carica totale del fascio sarà sei volte la carica di un protone, ovvero: $$q=6\cdot 1.6\cdot 10^{-19}C$$
Inoltre, la massa di un isotopo è dato dal prodotto del suo numero di massa e della massa di un singolo protone. Nel nostro caso, gli isotopi $^{16}0$ e $^{18}0$ hanno massa rispettivamente: $$\begin{eqnarray*} m_{16} &=& 16\cdot m_p\\ m_{18} &=& 18\cdot m_p\end{eqnarray*}$$
Dato che la forza di Lorentz provocata dal campo magnetico è una forza conservativa, possiamo applicare la conservazione dell'energia considerando che l'energia cinetica iniziale e l'energia potenziale finale del fascio siano entrambe nulle essendo nulle la velocità iniziale del fascio e la differenza di potenziale finale a cui è soggetto il fascio: $$E_p^i=E_{cin}^f$$
Per l'isotopo $^{16}0$ otteniamo dunque: $$qV=\frac{1}{2}m_{16}v_{16}^2$$ da cui $$v_{16}=\sqrt{\frac{2qV}{m_{16}}}$$
Mentre invece, per l'isotopo $^{18}0$ otteniamo: $$qV=\frac{1}{2}m_{18}v_{18}^2$$ da cui $$v_{18}=\sqrt{\frac{2qV}{m_{18}}}$$
La forza di Lorentz a cui sono soggetti gli isotopi dopo essere entrati nel campo magnetico in modo perpendicolare al campo stesso è: $$F_l=qvB$$ Applicando il secondo principio di Newton ($F=m\cdot a$) e ricordando che una particella che entra in modo perpendicolare al campo magnetico, si muove di moto circolare uniforme, possiamo eguagliare la forza di Lorentz con la forza centripeta: $$F_l=m\cdot a\ \Rightarrow\ qvB=m\frac{v^2}{r}\ \Rightarrow\ qB=m\frac{v}{r}$$ essendo $r$ il raggio della traiettoria circolare. Applichiamo ques'ultima equazione per i due isotopi in modo da ricavare i raggi delle loro traiettorie: $$\begin{eqnarray*} qB &=& m_{16}\frac{v_{16}}{r_{16}}\\ qB &=& m_{18}\frac{v_{18}}{r_{18}}\end{eqnarray*}$$ ossia $$\begin{eqnarray*} r_{16}&=&\frac{m_{16}\cdot v_{16}}{qB}\\ r_{18}&=&\frac{m_{18}\cdot v_{18}}{qB}\end{eqnarray*}$$
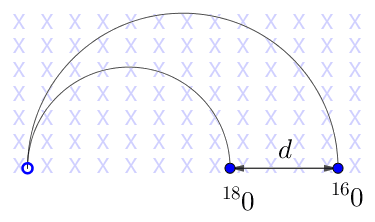
Guardando l'immagine sopra, i due isotopi, dopo aver compiuto mezza circonferenza, si trovano ad una distanza tra loro pari alla differenza dei loro diametri: $$d=2r_{16}-2r_{18}$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare