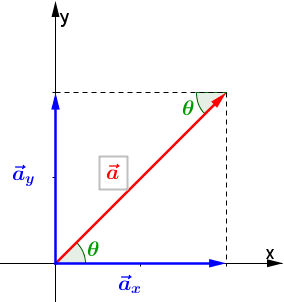
Un filo rettilineo indefinito è percorso dalla corrente $i(t) = i_0 e^{-t/\tau}$ , con $i_0= 10A$ e $\tau = 5 s$, e si trova nel piano di una spira rettangolare di lati $a = 6 cm$, $b = 12 cm$, alla distanza $r = 4 cm$ dal lato più vicino parallelo al filo, come mostrato in figura. Calcolare la f.e.m. indotta nella spira e la carica $q$ che percorre la spira nell’intervallo di tempo da zero a $\infty$, se essa ha una resistenza $R= 2\Omega$.

Per la legge di Biot-Savart, il campo magnetico generato dal filo indefinito percorso dalla corrente $i(t)$ in un punto posto a distanza x è: $$B(t)=\frac{\mu_0i(t)}{2\pi x}$$
Integrando il campo magnetico sulla superficie della spira rettangolare, si ottiene il flusso tagliato dalla spira: $$\begin{eqnarray*} \Phi(t) &=& \int B\ dS=\int_0^b dz\int_r^{r+a}B(t)\ dx=b\int_r^{r+a}\frac{\mu_0i(t)}{2\pi x}=\\ &=& \frac{b\mu_0i(t)}{2\pi}\left[ln(r+a)-ln(r)\right]=\frac{b\mu_0i(t)}{2\pi}\cdot ln\left(1+\frac{a}{r}\right)\end{eqnarray*}$$
La f.e.m. indotta si calcola facilmente derivando rispetto al tempo tale flusso: $$\varepsilon_{ind}=-\frac{d\Phi(t)}{dt}=-\frac{b\mu_0}{2\pi}\cdot i'(t)\cdot ln\left(1+\frac{a}{r}\right)$$
Supposta $R$ la resistenza della spira, la corrente in essa indotta è quindi: $$i_{ind}(t)=\frac{\varepsilon_{ind}}{R}=-\frac{b\mu_0}{2\pi R}\cdot i'(t)\cdot ln\left(1+\frac{a}{r}\right)$$
E infine, la carica $q(t)$ che percorre la spira nell'intervallo di tempo $(0, +\infty)$ coincide con l'integrale della corrente indotta esteso a tale intervallo: $$q(t)=\int_0^{+\infty}i_{ind}(t)\ dt$$

10.000 eserciziformazione completa
Eserciziari di Matematica Generale, Analisi I e II, Statistica, Fisica e Algebra Lineare