In statistica descrittiva e calcolo delle probabilità, le frequenze cumulate sono molto importanti perché ci forniscono informazioni utili sulla distribuzione del carattere oggetto di studio. Infatti, vengono utilizzate per il calcolo dei quartili e soprattutto della mediana.
Clicca nel bottone qui in basso per accedere alla sezione degli esercizi svolti.
Le frequenze cumulate si ottengono a partire dalle frequenze assolute o dalle frequenze relative che ti ho spiegato in dettaglio qui (fai click!).
Qui di seguito invece ti mostro come calcolare tali frequenze con degli esempi numerici.
Frequenze cumulate assolute
Facendo riferimento all'esempio n. 2 di questo articolo, calcolare le frequenze cumulate assolute significa appunto calcolare il totale cumulato delle frequenze assolute. Guarda la figura sottostante e i calcoli svolti
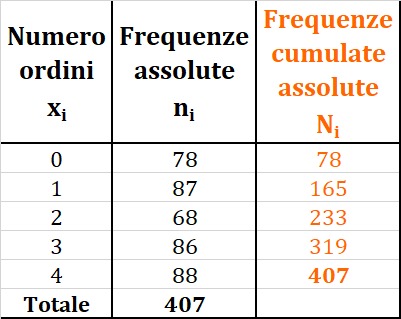
$$\begin{eqnarray*}N_1 &=& n_1=78\\N_2 &=& N_1+n_2=78+87=165\\ N_3 &=& N_2+n_3=165+68=233\\ N_4 &=& N_3+n_4=233+86=319\\ N_5 &=& N_4+n_5=319+88=407\end{eqnarray*}$$
Nota che la prima frequenza cumulata assoluta è sempre uguale alla prima frequenza assoluta, mentre l'ultima frequenza cumulata assoluta coincide con il totale delle frequenze assolute.
Frequenze cumulate relative
Se invece di cumulare le frequenze assolute cumuliamo le frequenze relative, allora otteniamo le frequenze cumulate relative:

$$\begin{eqnarray*}F_1 &=& f_1=78\\F_2 &=& F_1+f_2=78+87=165\\ F_3 &=& F_2+f_3=165+68=233\\ F_4 &=& F_3+f_4=233+86=319\\ F_5 &=& F_4+f_5=319+88=407\end{eqnarray*}$$
Stavolta nota che l'ultima frequenza cumulata relativa è pari a 1.
Frequenze cumulate percentuali
Le frequenze cumulate percentuali si ottengono moltiplicando per 100% le cumulate relative:
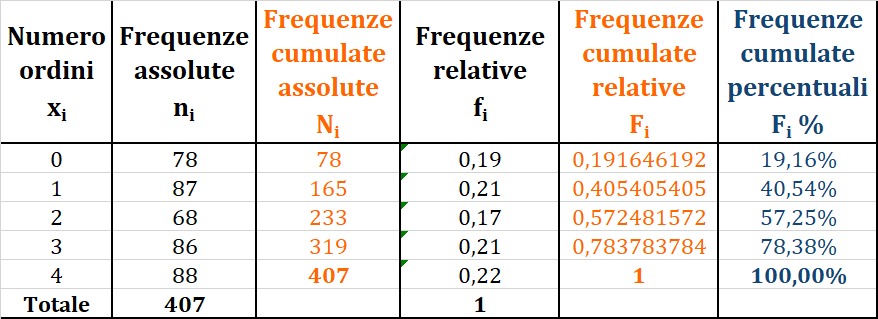
Frequenze retrocumulate
Le frequenze retrocumulate si ottengono cumulando le frequenze in ordine inverso rispetto a quello usato per calcolare le frequenze cumulate. Qui sotto ho calcolato le frequenze retrocumulate assolute, relative e percentuali relative all'esempio precedente:
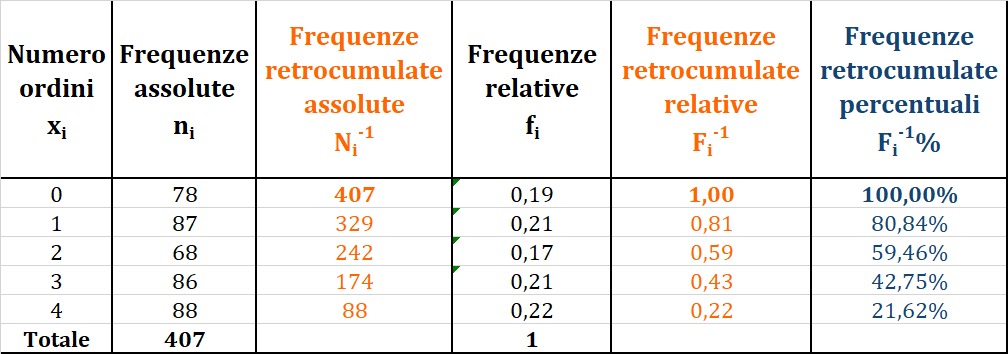
Ad esempio, le frequenze assolute sono state calcolate partendo dall'ultima frequenza assoluta (88) e procedendo verso l'alto, ossia:
$$\begin{eqnarray*}N_5 &=& n_5=88\\N_4 &=& N_5+n_4=88+86=174\\ N_3 &=& N_4+n_3=174+68=242\\ N_2 &=& N_3+n_2=242+87=329\\ N_1 &=& N_2+n_1=329+78=407\end{eqnarray*}$$
Come puoi notare dalla tabella qui sopra la prima frequenza retrocumulata assoluta è pari al totale delle frequenze assolute, la prima frequenza retrocumulata relativa vale 1 mentre la prima frequenza retrocumulata percentuale è uguale a 100%.



