In questo articolo abbiamo visto che nell'ambito della statistica descrittiva, la distribuzione di frequenza assume un ruolo molto importare perchè rappresenta il modo più comodo per organizzare i dati grezzi raccolti in seguito a una indagine statistica.
In questa lezione ti parlo di alcuni tipi di frequenze che si usano in statistica, ovvero:
- Frequenze assolute
- Frequenze relative
- Frequenze relative percentuali
Frequenze assolute
Le prime, in realtà, sono state già trattate nella lezione sulla distribuzione di frequenza. Queste sono definite come il numero di occorrenze delle varie modalità (o valori) della variabile studiata.
Supponiamo che il carattere $X$ presenta le seguenti modalità (o ciò che è lo stesso assume i seguenti valori): $$1,2,1,-3,0,-1,2,2,0,-3$$. La tabella con le frequenze assolute è quindi:

Frequenze relative
Le frequenze assolute da sole non riescono a dare un'idea sulla proporzione con cui ogni modalità compare all'interno della distribuzione $X$. Per questo esiste la frequenza relativa che è data dal rapporto tra la frequenza assoluta e la somma delle frequenze. In formule:
$$f_i=\cfrac{n_i}{n}$$
Di seguito, tramite un esempio, ti spiego come calcolare le frequenze relative
Supponi di avere la seguente tabella di frequenza del numero di ordini effettuati da un campione di 407 famiglie nel giorno del Black Friday

Calcoliamo le frequenze relative $f_i$ per ogni valore $x_i$:
$$\begin{eqnarray*} f_1 &=& \cfrac{78}{407}\\ f_2 &=& \cfrac{87}{407}\\ f_3 &=& \cfrac{68}{407}\\ f_4 &=& \cfrac{86}{407}\\ f_5 &=& \cfrac{88}{407} \end{eqnarray*}$$
Aggiungiamo le frequenze relative accanto a quelle assolute in tabella:

Nota che il totale delle frequenze relative è sempre 1.
Frequenze relative percentuali
Una volta calcolate le frequenze relative possiamo (ci conviene) calcolare anche le frequenze relative percentuali per ottenere appunto la proporzione percentuale di ogni modalità o valore della variabile in esame. Per calcolare le frequenze percentuali basta moltiplicare per $100\%$ le frequenze relative. Facendo riferimento all'esempio precedente, nell'ultima colonna della tabella sono state calcolate le frequenze percentuali:
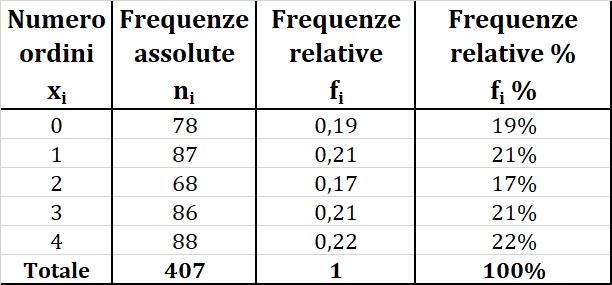
Dalle frequenze relative percentuali possiamo ricavare informazioni in più riguardo la distribuzione degli ordini, come ad esempio, il fatto che la maggior parte delle famiglie intervistate ha effettuato 4 ordini dato che a questo valore è associata la frequenza percentuale più grande (22%).
Clicca nel bottone qui sotto per scaricare esercizi sulle frequenze relative e percentuali ai fini del calcolo di indici di posizione e di dispersione.



