Una macchina termica irreversibile lavora con una mole di gas perfetto monoatomico descrivendo il ciclo costituito da 3 trasformazioni (vedi figura) sapendo che $V_A=V_C=5dm^3$, $V_B=15dm^3$, $P_A=13atm$, $P_B=4.5atm$. Si calcoli:
PUNTO a)
Per prima cosa, calcoliamo le temperature nei punti A,B e C tramite la legge dei gas perfetti: $$PV=nRT\ \Rightarrow\ T=\frac{PV}{nR}$$ $$\begin{eqnarray} T_A &=& \frac{P_AV_A}{nR}=\frac{13\cdot 5}{1\cdot 0.082}=792.68°K\\ T_B &=& \frac{P_BV_B}{nR}=\frac{4.5\cdot 15}{1\cdot 0.082}=823.17°K\\ T_C &=& \frac{P_CV_C}{nR}=\frac{4.5\cdot 5}{1\cdot 0.082}=274.39°K\end{eqnarray}$$
Pressione, volume e temperatura nei punti A, B e C sono riassunti nella tabella sottostante
Consideriamo la trasformazione AB. Sapendo che il calore specifico per i gas monoatomici a volume costante è $c_v=\frac{3}{2}R$, la variazione di energia interna sarà: $$\Delta U_{AB}=nc_v(T_B-T_A)=1\cdot\frac{3}{2}\cdot 8.314(823.17-792.68)=380.24J$$
Il lavoro è dato, invece dall'area sottesa dalla curva P nel tratto AB, ovvero, la somma dell'area del triangolo e del rettangolo che si vengono a formare: $$\begin{array}{l} L_{AB}&=\frac{(V_B-V_C)(P_A-P_C)}{2}+(V_B-V_C)\cdot P_C=\\ &=\frac{(15-5)\cdot 10^{-3}(13-4.5)\cdot 1.01\cdot 10^5}{2}+(15-5)\cdot 10^{-3}\cdot 4.5\cdot 1.01\cdot 10^5=8837.5J\end{array}$$
Dal 1° principio della termodinamica calcoliamo il calore in questa trasformazione: $$Q_{AB}=\Delta U_{AB}+L_{AB}=380.24+8837.5=9217.74J$$
Consideriamo la trasformazione BC. Osservando che essa è isobara e che il calore specifico a pressione costante per i gas monoatomici è $c_p=\frac{5}{2}R$, si ha: $$Q_{BC}=n\cdot c_p\cdot (T_C-T_B)=1\cdot\frac{5}{2}8.314(274.39-823.17)=-11406.39J$$
Come fatto per la trasformazione AB, il lavoro svolto nella trasformazione BC è dato dall'area del rettangolo sotto la curva nel tratto BC. A tale calcolo va aggiunto un segno meno perchè il lavoro della compressione di un gas è negativo: $$L_{BC}=-(V_B-V_C)\cdot P_C=-(15-5)\cdot 10^{-3}\cdot 4.5\cdot 1.01\cdot 10^5=-4545J$$
Dal 1° principio della termodinamica calcoliamo la variazione di energia interna in questa trasformazione: $$\Delta U_{BC}=Q_{BC}-L_{BC}=-11406.39+4545=-6861.39J$$
Infine, consideriamo la trasformazione CA irreversibile. Poichè si tratta di una trasformazione isocora, $L_{CA}=0J$ e la variazione di energia interna coincide con il calore scambiato: $$\begin{eqnarray}Q_{CA}&=&\Delta U_{CA}=n\cdot c_v(T_A-T_C)=\\ &=&\frac{3}{2}\cdot 8.314(792.68-274.39)=6463.59J$$
Sommando le quantità di calore, lavoro e variazione di energia interna di ogni trasformazione, otteniamo: $$\begin{eqnarray} Q_{tot} &=& Q_{AB}+Q_{BC}+Q_{CA}=4274.94J\\ \Delta U_{tot} &=& \Delta U_{AB}+\Delta U_{BC}+\Delta U_{CA}=-17.56J\\ L_{tot} &=& L_{AB}+L_{BC}+L_{CA}=4292.5J\end{eqnarray}$$
Di seguito uno schema riassuntivo di quanto trovato.
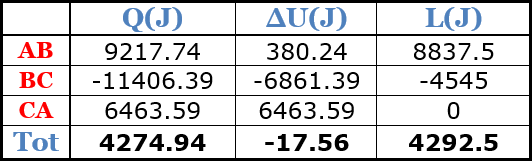
E' importante ricordare che la variazione di energia interna in un ciclo deve essere nulla, da cui, per il primo principio della termodinamica avremo che il lavoro totale eguaglia il calore scambiato nel ciclo. Osserviamo che le varie approssimazioni fatte durante i calcoli non permettono di ottenere precisamente tali valori ma ci avviciniamo a loro.
PUNTO b)
Il rendimento della macchina termica può essere calcolato facendo il rapporto tra il lavoro totale svolto dal ciclo e il calore totale assorbito ($Q_{AB}+Q_{CA}$): $$\eta=\frac{L_{tot}}{Q_{ass}}=\frac{4292.5}{9217.74+4274.94}=0.32=32\%$$
PUNTO c)
Calcoliamo la variazione di entropia del sistema in ciascuna trasformazione: $$\begin{array}{l} \Delta S_{AB}^s &= n\cdot c_v\cdot \ln\frac{T_B}{T_A}+n\cdot R\cdot \ln\frac{V_B}{V_A}=\\ &=1\cdot\frac{3}{2}\cdot 8.314\cdot\ln\frac{823.17}{792.68}+1\cdot 8.314\cdot\ln\frac{15}{5}=9.60\\ \Delta S_{BC}^s &= n\cdot c_p\cdot \ln\frac{T_C}{T_B}=1\cdot\frac{5}{2}\cdot 8.314\cdot\ln\frac{274.39}{823.17}=-22.83\\ \Delta S_{CA}^s &= n\cdot c_v\cdot \ln\frac{T_A}{T_C}=1\cdot\frac{3}{2}\cdot 8.314\cdot\ln\frac{792.68}{274.39}=13.23\end{array}$$
Le variazioni di entropia dell'universo nelle trasformazioni reversibili sono sempre nulle $$\begin{array}{l} \Delta S_{AB}^u=0\\ \Delta S_{BC}^u=0\end{array}$$
Di conseguenza, le variazioni di entropia dell'ambiente sono opposte alle variazioni di entropia del sistema per quanto riguarda le trasformazioni reversibili AB e BC $$\begin{array}{l} \Delta S_{AB}^a &= -\Delta S_{AB}^s = -9.60\\ \Delta S_{BC}^a &= -\Delta S_{BC}^s = 22.83\end{array}$$
Mentre, invece, nella trasformazione irreversibile CA, poichè l'ambiente cede calore al sistema, l'entropia sarà negativa è uguale a: $$\Delta S_{CA}^a=-\frac{Q_{CA}}{T_A}=-\frac{4274.94}{792.68}=-5.39$$
Infine la variazione di entropia dell'universo per la trasformazione irreversibile è data da: $$\Delta S_{CA}^u=\Delta S_{CA}^s+\Delta S_{CA}^a=13.23-5.39=7.84$$
Di seguito uno schema riassuntivo di quanto trovato.
